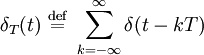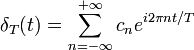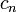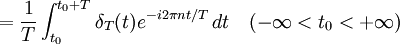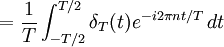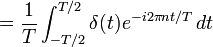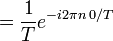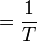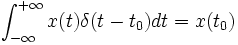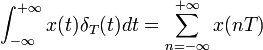Peigne de dirac

Peigne de dirac

Peigne de Dirac

La fonction peigne de Dirac est une série infinie de fonctions de Dirac espacées de T.

En mathématiques, la fonction peigne de Dirac, ou fonction shah (d'après la lettre cyrillique Ш), est une somme de fonctions de Dirac espacées de T :

\delta_T (t) \ \stackrel{\mathrm{def}}{=}\ \sum_{k=-\infty}^{\infty} \delta(t - k T)

Cette fonction est particulièrement utile dans les problèmes d'échantillonnage, remplacement d'une fonction continue par une suite de valeurs de la fonction séparées par un pas de temps T (voir Théorème d'échantillonnage de Nyquist-Shannon).

Séries de Fourier

Cette fonction est T-périodique, on peut donc calculer la série de Fourier associée. La série de Fourier complexe d'une telle fonction s'écrit :

\delta_T(t) = \sum_{n=-\infty}^{+\infty} c_n e^{i 2 \pi n t/T} \

où les coefficients de Fourier cn sont

c_n\, = \frac{1}{T} \int_{t_0}^{t_0 + T} \delta_T(t) e^{-i 2 \pi n t/T}\, dt \quad ( -\infty < t_0 < +\infty ) \
= \frac{1}{T} \int_{-T/2}^{T/2} \delta_T(t) e^{-i 2 \pi n t/T}\, dt \
= \frac{1}{T} \int_{-T/2}^{T/2} \delta(t) e^{-i 2 \pi n t/T}\, dt \
= \frac{1}{T} e^{-i 2 \pi n \, 0/T} \
= \frac{1}{T} \

La série s'écrit donc :

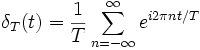\delta_T(t) = \frac{1}{T}\sum_{n=-\infty}^{\infty} e^{i 2 \pi n t/T}.

En oubliant toute rigueur, on peut constater que les termes complexes de la série sont représentés dans le plan complexe par des vecteurs unités en rotation. Si t est un multiple de la période T, on obtient une somme d'une infinité de termes égaux à un ; sinon les vecteurs tournent indéfiniment autour du zéro en donnant une somme nulle.

Propriété fondamentale du peigne de Dirac

La propriété fondamentale de la fonction de Dirac

\int_{-\infty}^{+\infty} x(t) \delta(t-t_0) dt = x(t_0)

conduit à la propriété fondamentale du peigne

\int_{-\infty}^{+\infty} x(t) \delta_T(t) dt = \sum_{n=-\infty}^{+\infty} x(nT)

Le calcul approché d'une intégrale par la méthode des rectangles est équivalent au calcul de l'intégrale de la fonction multipliée par un peigne de Dirac.

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Peigne de Dirac ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Peigne de dirac de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Peigne de Dirac — La fonction peigne de Dirac est une série infinie de fonctions de Dirac espacées de T. En mathématiques, la fonction peigne de Dirac, ou fonction shah (d après la lettre cyrillique Ш), est une somme de fonctions de Dirac espacées de T  …   Wikipédia en Français

  • Dirac — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Patronyme Paul Dirac (1902 1984), physicien et mathématicien britannique, suite à ses travaux en mécanique quantique, a donné son nom à plusieurs objets… …   Wikipédia en Français

  • Peigne (homonymie) — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Un peigne est un outil qui sert à remettre les cheveux en ordre. Par extension, on appelle peigne certains outils qui possèdent des tiges parallèles… …   Wikipédia en Français

  • Paul Dirac — Paul Adrien Maurice Dirac Naissance 8 août 1902 Bristol (Angleterre) Décès 20 octobre 1984 (à 82 ans) …   Wikipédia en Français

  • Delta de Dirac — Distribution de Dirac La distribution de Dirac, aussi appelée par abus de langage fonction δ de Dirac, introduite par Paul Dirac, peut être informellement considérée comme une fonction δ qui prend une « valeur » infinie en 0, et la… …   Wikipédia en Français

  • Distribution De Dirac — La distribution de Dirac, aussi appelée par abus de langage fonction δ de Dirac, introduite par Paul Dirac, peut être informellement considérée comme une fonction δ qui prend une « valeur » infinie en 0, et la valeur zéro partout… …   Wikipédia en Français

  • Distribution de dirac — La distribution de Dirac, aussi appelée par abus de langage fonction δ de Dirac, introduite par Paul Dirac, peut être informellement considérée comme une fonction δ qui prend une « valeur » infinie en 0, et la valeur zéro partout… …   Wikipédia en Français

  • Fonction Dirac — Distribution de Dirac La distribution de Dirac, aussi appelée par abus de langage fonction δ de Dirac, introduite par Paul Dirac, peut être informellement considérée comme une fonction δ qui prend une « valeur » infinie en 0, et la… …   Wikipédia en Français

  • Fonction de Dirac — Distribution de Dirac La distribution de Dirac, aussi appelée par abus de langage fonction δ de Dirac, introduite par Paul Dirac, peut être informellement considérée comme une fonction δ qui prend une « valeur » infinie en 0, et la… …   Wikipédia en Français

  • Fonction de dirac — Distribution de Dirac La distribution de Dirac, aussi appelée par abus de langage fonction δ de Dirac, introduite par Paul Dirac, peut être informellement considérée comme une fonction δ qui prend une « valeur » infinie en 0, et la… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”