POMDP

POMDP

Processus de décision markovien partiellement observable

Un Processus de décision markovien partiellement observable (POMDP) est un modèle stochastique issu de la théorie de la décision et de la théorie des probabilités. Les modèles de cette famille sont, entre autres, utilisés en intelligence artificielle pour le contrôle de systèmes complexes comme des agents intelligents.

Ce modèle est dérivé des Processus de décision markoviens (MDP). La différence est que, dans un POMDP, l'incertitude est double. Non seulement l'effet des actions que l'on entreprend est incertain, mais de plus, on ne dispose que d'indices pour connaitre l'état dans lequel on se trouve, et donc pour décider. Ces indices sont appelés des observations et en ce sens, les POMDP sont des Modèles de Markov Cachés (HMM) particuliers, dans lesquels on dispose d'actions probabilistes.

Sommaire

Définition formelle

Un POMDP est un tuple 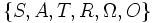\{ S, A, T, R, \Omega, O \}\, où :

  • S = \{ s_0, \cdots , s_{ |S-1| } \} \, est l'ensemble fini discret des états possibles du système à contrôler (il s'agit des états cachés du processus).
  • A = \{ a_0, \cdots , a_ {|A-1| } \} \, est l'ensemble fini discret des actions que l'on peut effectuer pour contrôler le système
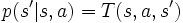  • T : S \times A \times S \to [ 0 ; 1 ]\, est la fonction de transition du système en réaction aux actions de contrôle. Dans le cas général, la fonction T est probabiliste et donne la probabilité p (s' | s, a) = T (s, a, s') \, que le système passe de l'état s à l'état s' lorsque l'on choisit d'effectuer l'action a.
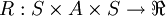  • R : S \times A \times S \to \Re est la fonction de récompense. Elle indique la valeur réelle obtenue lorsque l'on effectue l'action a dans l'état s et que l'on arrive dans l'état s'.
  • \Omega = \{ \omega_0 \cdots \omega_{ |\Omega-1|} \} est un ensemble de symboles que l'on peut observer.
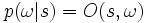  • O : S \times \Omega \to [0;1] est une fonction d'observation qui à un état donné associe la probabilité p (\omega | s) = O (s , \omega) \, d'observer un symbole donné.

Note : Il existe des variantes dans les quelles les récompenses peuvent dépendre des actions ou des observations. Les observations peuvent également dépendre des actions effectuées.

Approches

Il existe deux grands types d'approches pour s'attaquer à un problème POMDP.

  • On peut chercher à déterminer de la façon la plus certaine possible quel est l'état dans lequel on se trouve (en maintenant à jour une distribution de probabilité sur les états appelée belief-state)
  • On peut travailler directement sur les observations [2] de Ω sans considérer l'état caché. Cela n'est pas sans poser de problèmes car des observations similaires peuvent être obtenues dans des états différents (par exemple, avec l'observation locale des carrefours dans un labyrinthe, on peut très bien tomber sur deux carrefours en forme de T). Une approche possible pour discriminer ces observations consiste à garder une mémoire des observations rencontrées par le passé (dans ce cas, on perd la propriété markovienne).

Articles connexes

Références

  1. Kaebling L. P., Littman M. L., Cassandra A. R., Planning and Acting in Partially Observable Stochastic Domains, Artificial Intelligence, vol. 101, num. 1–2, pp. 99-134, 1998.
  2. McCallum A. K., Reinforcement learning with selective perception and hidden state, PhD thesis, University of Rochester, Computer Science Dept., 1996.

Liens externes

Ce document provient de « Processus de d%C3%A9cision markovien partiellement observable ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article POMDP de Wikipédia en français (auteurs)

Игры ⚽ Поможем решить контрольную работу

Regardez d'autres dictionnaires:

  • Monte Carlo POMDP — In the class of Markov decision process algorithms, the Monte Carlo POMDP (MC POMDP) is the particle filter version for the partially observable Markov decision process (POMDP) algorithm. In MC POMDP, particles filters are used to update and… …   Wikipedia

  • Partially observable Markov decision process — A Partially Observable Markov Decision Process (POMDP) is a generalization of a Markov Decision Process. A POMDP models an agent decision process in which it is assumed that the system dynamics are determined by an MDP, but the agent cannot… …   Wikipedia

  • Processus de decision markovien partiellement observable — Processus de décision markovien partiellement observable Un Processus de décision markovien partiellement observable (POMDP) est un modèle stochastique issu de la théorie de la décision et de la théorie des probabilités. Les modèles de cette… …   Wikipédia en Français

  • Processus de décision markovien partiellement observable — Un Processus de décision markovien partiellement observable (POMDP) est un modèle stochastique issu de la théorie de la décision et de la théorie des probabilités. Les modèles de cette famille sont, entre autres, utilisés en intelligence… …   Wikipédia en Français

  • Markov decision process — Markov decision processes (MDPs), named after Andrey Markov, provide a mathematical framework for modeling decision making in situations where outcomes are partly random and partly under the control of a decision maker. MDPs are useful for… …   Wikipedia

  • Automated planning and scheduling — is a branch of artificial intelligence that concerns the realization of strategies or action sequences, typically for execution by intelligent agents, autonomous robots and unmanned vehicles. Unlike classical control and classification problems,… …   Wikipedia

  • Preference elicitation — refers to the problem of developing a decision support system capable of generating recommendations to a user, thus assisting him in decision making. It is important for such a system to model user s preferences accurately, find hidden… …   Wikipedia

  • Dialog system — An automated online assistant on a website an example where dialog systems are major components. A dialog system or conversational agent (CA) is a computer system intended to converse with a human, with a coherent structure. Dialog systems have… …   Wikipedia

  • Chaine De Markov — Chaîne de Markov Selon les auteurs, une chaîne de Markov est de manière générale un processus de Markov à temps discret ou un processus de Markov à temps discret et à espace d états discret. En mathématiques, un processus de Markov est un… …   Wikipédia en Français

  • Chaine de Markov — Chaîne de Markov Selon les auteurs, une chaîne de Markov est de manière générale un processus de Markov à temps discret ou un processus de Markov à temps discret et à espace d états discret. En mathématiques, un processus de Markov est un… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”