Ordre (algèbre)

Ordre (algèbre)

Degré (mathématiques)

Page d'aide sur l'homonymie Pour les articles homonymes, voir Degré.

De manière générale, un degré indique un incrément, une quantité définie qui s'ajoute. On parle des degrés d'une échelle ou d'un escalier pour désigner les barreaux ou les marches (on monte d'une quantité donnée à chaque pas).

Sommaire

Polynômes et fractions

Degré d'un polynôme

À une indéterminée

Article détaillé : Construction de l'anneau des polynômes.

Soit A un anneau. L'anneau des polynômes à une indéterminée sur A est A[X], soit P un polynôme à coefficients dans A.

Le degré de P, noté deg(P) ou 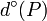d^\circ(P) est défini par :

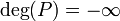
  • Si P = 0, \deg(P) = -\infty
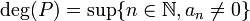
  • Sinon, pour P = anXn + an − 1Xn − 1 + ... + a1X + a0, on définit : \deg(P)= \sup \{n \in \N, a_{n} \ne 0 \}

Par exemple, deg(3X5 − 2X4 + 8X − 2) = 5

En plusieurs indéterminées

Article détaillé : polynôme en plusieurs indéterminées.

Soient A un anneau et 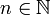n \in \N. L'anneau des polynômes à n indéterminées sur A est A[X1,X2,...,Xn]

Le degré du polynôme nul est toujours -\infty.

Sinon on considère l'ensemble des « sommes des exposants des indéterminées » dans chaque terme. Le degré du polynôme est alors le plus grand élément de cet ensemble.

Par exemple : dans A[X,Y],deg(X2Y2 + 3X3 + 4Y) = 4

Degré d'une fraction rationnelle

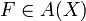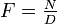Soit A un anneau commutatif, unitaire, intègre. Le corps des fractions rationnelles à une indéterminée sur A est A(X). Soit F \in A(X). Il existe N \in A[X] et D \in A[X] \setminus \{ 0 \} tel que F=\tfrac{N}{D}.

La grandeur 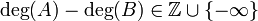\deg(A)-\deg(B) \in \mathbb Z \cup \{-\infty\} est indépendante du représentant 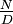\tfrac{N}{D} choisi pour F.

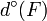On définit alors deg(F) = deg(A) − deg(B), noté deg(F) ou d^\circ(F).

Propriétés du degré

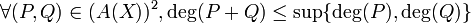
  • \forall (P,Q) \in (A(X))^2, \deg(P+Q)\leq \sup \{\deg(P) , \deg(Q) \}
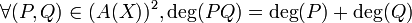
  • Si A est intègre, \forall (P,Q) \in (A(X))^2, \deg(PQ)=\deg(P) + \deg(Q)

Graphe et sommet

En théorie des graphes, le degré d'un sommet est le nombre d'arêtes issues de ce sommet.

Voir aussi

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Degr%C3%A9 (math%C3%A9matiques) ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Ordre (algèbre) de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Algebre d'un groupe fini — Algèbre d un groupe fini En mathématiques, l algèbre d un groupe fini s inscrit dans le cadre de la théorie des représentations d un groupe fini. Une algèbre d un groupe fini est la donnée d un groupe fini, d un espace vectoriel de dimension l… …   Wikipédia en Français

  • Algèbre D'un Groupe Fini — En mathématiques, l algèbre d un groupe fini s inscrit dans le cadre de la théorie des représentations d un groupe fini. Une algèbre d un groupe fini est la donnée d un groupe fini, d un espace vectoriel de dimension l ordre du groupe et d une… …   Wikipédia en Français

  • Algebre de Clifford — Algèbre de Clifford En mathématiques, les algèbres de Clifford sont des algèbres associatives importantes au sein des théories des formes quadratiques, des groupes orthogonaux et en physique. Elles peuvent être vues comme l une des… …   Wikipédia en Français

  • Algèbre De Clifford — En mathématiques, les algèbres de Clifford sont des algèbres associatives importantes au sein des théories des formes quadratiques, des groupes orthogonaux et en physique. Elles peuvent être vues comme l une des généralisations possibles des… …   Wikipédia en Français

  • Algèbre de Clifford du plan euclidien) — Algèbre de Clifford En mathématiques, les algèbres de Clifford sont des algèbres associatives importantes au sein des théories des formes quadratiques, des groupes orthogonaux et en physique. Elles peuvent être vues comme l une des… …   Wikipédia en Français

  • Algèbre de clifford — En mathématiques, les algèbres de Clifford sont des algèbres associatives importantes au sein des théories des formes quadratiques, des groupes orthogonaux et en physique. Elles peuvent être vues comme l une des généralisations possibles des… …   Wikipédia en Français

  • ALGÈBRE — L’algèbre au sens moderne, à savoir l’étude des structures algébriques indépendamment de leurs réalisations concrètes, ne s’est dégagée que très progressivement au cours du XIXe siècle, en liaison avec le mouvement général d’axiomatisation de… …   Encyclopédie Universelle

  • Algèbre Nouvelle — L’algèbre nouvelle ou analyse spécieuse est un projet de formalisation de l’algèbre tenté par François Viète et ses successeurs. Il marque le début de la formalisation algébrique (fin XVIe début XVIIe siècle). Sommaire 1 Idées générales 2 …   Wikipédia en Français

  • Algebre de Boole (logique) — Algèbre de Boole (logique) Pour les articles homonymes, voir Algèbre de Boole. L algèbre de Boole, ou calcul booléen, est la partie des mathématiques, de la logique et de l électronique qui s intéresse aux opérations et aux fonctions sur les… …   Wikipédia en Français

  • Algèbre De Boole (Logique) — Pour les articles homonymes, voir Algèbre de Boole. L algèbre de Boole, ou calcul booléen, est la partie des mathématiques, de la logique et de l électronique qui s intéresse aux opérations et aux fonctions sur les variables logiques. Plus… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”