Optimum de pareto

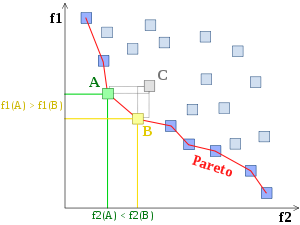
Optimum de pareto

Optimum de Pareto

Exemple de frontière d'efficacité de Pareto : si les situations préférables sont celles où f1 et f2 sont les plus faibles, le Point C n'est pas sur la frontière de Pareto parce qu'il est dominé par les points A et B. Les points A et B sont tous les deux efficaces.

En économie, un optimum de Pareto est un état dans lequel on ne peut pas améliorer le bien-être d’un individu sans détériorer celui d’un autre.

La notion d'optimum de Pareto permet de diviser en deux l'ensemble des états possibles de la société. On peut ainsi distinguer :

  • ceux qui sont uniformément améliorables : il est possible d'augmenter le bien-être de certains individus sans réduire celui des autres.
  • ceux qui ne sont pas uniformément améliorables : l'augmentation du bien-être de certains individus implique la réduction du bien-être d'au moins un autre individu.

Ce sont ces derniers états que l'on désigne comme optimaux au sens de Pareto, ou Pareto-optimaux.

De nombreux états possibles de la société sont des optima de Pareto. La notion d'optimum de Pareto ne permet pas de les comparer entre eux : il est nécessaire de faire appel à d'autres critères.

Pour cette raison, une situation d’optimalité « au sens de Pareto » n’est pas nécessairement une situation socialement "juste". Pour prendre un exemple extrême, une société où toutes les richesses appartiennent à un seul homme est un optimum de Pareto, car transférer une partie de ses richesses à d’autres personnes réduirait le bien-être d’au moins un individu. Par ailleurs, dans cette même situation, s’il devient possible de faire des changements qui augmenteraient le stock total de richesses de la société sans retirer de capital à cet homme, alors la situation n'est plus Pareto-optimale.

Il convient donc d’employer une terminologie rigoureuse et de parler d'état efficace « au sens de Pareto ».

Sommaire

Critère de Pareto et critère utilitariste

En cela, la notion d'optimum de Pareto est très éloignée du critère utilitariste de comparaison des états possibles de la société. Celui-ci, aussi appelé principe du plus grand bonheur, prend en effet en considération le bonheur global de la société, conçu comme l'agrégation des bien-être de tous les individus, et déclare qu'un état de la société est moralement préférable à un autre si son bonheur global est plus grand que le bonheur global dans le second état de société.

Le critère de Pareto et le critère utilitariste ne sont pas comparables. En effet :

  • deux états, tous deux optimaux au sens de Pareto, peuvent être distingués et hiérarchisés par le critère utilitariste : le bonheur global de ces deux états n'est pas, en général, le même.
  • si un état n'est pas optimal au sens de Pareto, alors il existe un autre état, optimal au sens de Pareto, qui est préférable ou égal au précédent pour tous les agents composant la société, sans exception. L'utilitarisme distingue également ces deux états : le bonheur global dans le deuxième état est plus grand que le bonheur global dans le premier.
  • par contre, il arrive qu'un état non-optimal au sens de Pareto soit considéré, suivant le critère utilitariste, comme égal à, ou meilleur, qu'un état optimal au sens de Pareto : autrement dit, un état de société uniformément améliorable peut, malgré sa perfectibilité, engendrer un bonheur global plus important que certains états de société non uniformément améliorables.

La détermination de l'optimum de Pareto

Si la définition d'un optimum de Pareto semble très simple, on peut avoir des difficultés à estimer les prix dits prix parétiens dans un modèle d'équilibre général.

Considérons un cadre économique où vivent i=I consommateurs, k=K entreprises et où j=L biens sont disponibles ou produits. On cherche à définir les allocations Pareto-optimales, c'est-à-dire les consommations (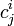c_j^i) et les productions (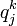q_j^k) de chaque bien pour chaque agent. Il n'est pas question dans une telle vision de gaspiller des biens et donc pour les firmes de produire une quantité supérieure à la quantité qu'elle pourra écouler sur le marché grace aux demandes individuelles. On peut donc écrire une première contrainte liant les demandes et les offres: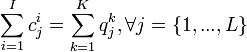

\sum_{i=1}^I c_j^i = \sum_{k=1}^K q_j^k , \forall j=\{1,...,L\}

Chaque consommateur i dispose d'une utilité ui, fonction de toutes ses consommations 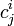c_j^i qu'il cherche à maximiser. On note 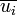\overline {u_i} l'utilité maximum possible.

Chaque entreprise k dispose d'un coût de production Ck fonction de toutes les productions 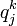q_j^k qu'elle cherche à minimiser. On note 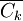\overline {C_k} le coût minimum possible.

Trouver l'optimum de Pareto revient à maximiser l'utilité du premier consommateur, sous les contraintes d'obtenir une utilité maximum pour les autres consommateurs et un coût minimum pour les entreprises. Il faut également que la première contrainte de non-gaspillage soit respectée. Le système suivant peut donc être défini:

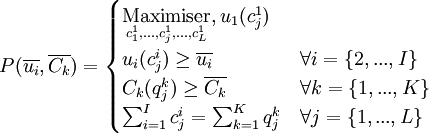
P(\overline {u_i},\overline {C_k}) = \begin{cases} \underset{c_1^1,...,c_j^1,...,c_L^1}{\text{Maximiser}} , u_1(c_j^1) \\ u_i(c_j^i) \ge \overline {u_i} & \forall i=\{ 2,...,I \} \\ C_k(q_j^k) \ge \overline {C_k} & \forall k=\{ 1,...,K \} \\ \sum_{i=1}^I c_j^i = \sum_{k=1}^K q_j^k & \forall j=\{1,...,L\} \end{cases}

Pour résoudre ce problème d'optimisation sous contrainte, il suffit de poser un lagrangien:

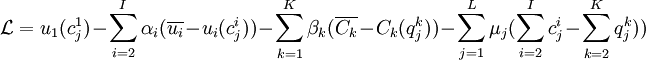
\mathcal{L} = u_1(c_j^1) - \sum_{i=2}^I \alpha_i (\overline{u_i} - u_i(c_j^i)) - \sum_{k=1}^K \beta_k (\overline{C_k} - C_k(q_j^k)) - \sum_{j=1}^L \mu_j (\sum_{i=2}^I c_j^i - \sum_{k=2}^K q_j^k))

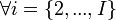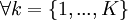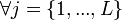Le lagrangien permet d'écrire L(KI) conditions \forall i=\{ 2,...,I \}, \forall k=\{ 1,...,K \} et \forall j=\{ 1,...,L \}:

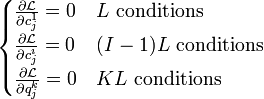
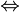
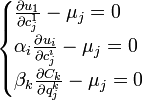
\begin{cases} \frac{\partial \mathcal{L}}{\partial c_j^1} = 0 & L \text{ conditions} \\ \frac{\partial \mathcal{L}}{\partial c_j^i} = 0 & (I-1)L \text{ conditions} \\ \frac{\partial \mathcal{L}}{\partial q_j^k} = 0 & KL \text{ conditions} \end{cases} \Leftrightarrow \begin{cases} \frac{\partial u_1}{\partial c_j^1} - \mu_j = 0 \\ \alpha_i \frac{\partial u_i}{\partial c_j^i} - \mu_j = 0 \\ \beta_k \frac{\partial C_k}{\partial q_j^k} - \mu_j = 0 \end{cases}

En résolvant, et en mettant tout au même dénominateur μ1, on obtient les relations suivantes:

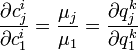
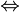
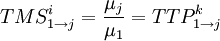
\frac{\partial c_j^i}{\partial c_1^i} = \frac{\mu_j}{\mu_1} = \frac{\partial q_j^k}{\partial q_1^k} \Leftrightarrow TMS_{1 \to j}^i = \frac{\mu_j}{\mu_1} = TTP_{1 \to j}^k

Les μj sont les prix parétiens cherchés. On constate qu'ils correspondent aux mêmes prix walrassiens déterminés par un équilibre général en concurrence pure et parfaite. Les TMS de chaque consommateur et les TTP de chaque producteur s'égalisent aux rapport des prix, et ce quel que soit le bien j.

Il s'agit de la démonstration mathématique du premier théorème du bien-être.

Optimum de Pareto et économie néo-classique

En vertu du premier théorème du bien-être, l’équilibre général en concurrence parfaite est un optimum de Pareto (c’est la référence à atteindre chez les néoclassiques). Cette notion est issue des travaux de Vilfredo Pareto qui lui a donné son nom.

Bibliographie

  • Alexis Jacquemin et Henry Tulkens, Fondements d'économie politique, De Boeck, Bruxelles, 2e édition, 1996, pp. 213-215.

Voir aussi

  • Portail de l’économie Portail de l’économie
Ce document provient de « Optimum de Pareto ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Optimum de pareto de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Optimum de Pareto — En économie, un optimum de Pareto, nommé d après l économiste italien Vilfredo Pareto, est un état de la société dans lequel on ne peut pas améliorer le bien être d’un individu sans détériorer celui d’un autre. Sommaire 1 Concept d optimum de… …   Wikipédia en Français

  • Optimum — de Pareto Exemple de frontière d efficacité de Pareto : si les situations préférables sont celles où f1 et f2 sont les plus faibles, le Point C n est pas sur la frontière de Pareto parce qu il est dominé par les points A et B. Les points A… …   Wikipédia en Français

  • Optimum économique — Optimum de Pareto Exemple de frontière d efficacité de Pareto : si les situations préférables sont celles où f1 et f2 sont les plus faibles, le Point C n est pas sur la frontière de Pareto parce qu il est dominé par les points A et B. Les… …   Wikipédia en Français

  • Pareto-Optimum — Pareto Optima (rot) einer 2dimensionalen Wertemenge (blau). Ein Pareto Optimum, auch Pareto Effizienz oder Pareto Menge, benannt nach dem Ökonomen und Soziologen Vilfredo Pareto (1848–1923), ist ein Zustand, in dem es nicht möglich ist, ein… …   Deutsch Wikipedia

  • Pareto-Superiorität — Pareto Optimum (rot) einer 2dimensionalen Wertemenge (blau). Ein Pareto Optimum, auch Pareto Effizienz oder Pareto Menge, benannt nach dem Ökonom und Soziologen Vilfredo Pareto (1848 1923), ist ein Zustand, in dem es nicht möglich ist, ein… …   Deutsch Wikipedia

  • Pareto-Verbesserung — Pareto Optimum (rot) einer 2dimensionalen Wertemenge (blau). Ein Pareto Optimum, auch Pareto Effizienz oder Pareto Menge, benannt nach dem Ökonom und Soziologen Vilfredo Pareto (1848 1923), ist ein Zustand, in dem es nicht möglich ist, ein… …   Deutsch Wikipedia

  • Pareto-besser — Pareto Optimum (rot) einer 2dimensionalen Wertemenge (blau). Ein Pareto Optimum, auch Pareto Effizienz oder Pareto Menge, benannt nach dem Ökonom und Soziologen Vilfredo Pareto (1848 1923), ist ein Zustand, in dem es nicht möglich ist, ein… …   Deutsch Wikipedia

  • Pareto-schlechter — Pareto Optimum (rot) einer 2dimensionalen Wertemenge (blau). Ein Pareto Optimum, auch Pareto Effizienz oder Pareto Menge, benannt nach dem Ökonom und Soziologen Vilfredo Pareto (1848 1923), ist ein Zustand, in dem es nicht möglich ist, ein… …   Deutsch Wikipedia

  • Pareto-unvergleichbar — Pareto Optimum (rot) einer 2dimensionalen Wertemenge (blau). Ein Pareto Optimum, auch Pareto Effizienz oder Pareto Menge, benannt nach dem Ökonom und Soziologen Vilfredo Pareto (1848 1923), ist ein Zustand, in dem es nicht möglich ist, ein… …   Deutsch Wikipedia

  • Pareto — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Vilfredo Pareto (1848 1923) était un sociologue et économiste italien, voir aussi Optimum de Pareto, ou encore Equilibre général boîte de Pareto… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”