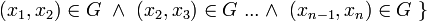- Operation sur des correspondances
-
Opération sur des correspondances
Une opération sur des correspondances permet de créer de nouvelles correspondances.
Sommaire
Correspondances et opérations ensemblistes
Les opérations purement ensemblistes sur les correspondances n’offrent aucun intérêt. Par exemple, la réunion ensembliste de deux correspondances n’est pas en général une correspondance.
En revanche, il est possible de définir des correspondances dont le graphe est le résultat d’opérations ensemblistes sur d’autres graphes :
Réunion
La réunion relationnelle de deux correspondances
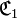 et
et 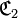 , notée :
, notée :- «
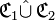 » ( lire « C1 union C2 » )
» ( lire « C1 union C2 » )
est la correspondance dont :
- - l’ensemble de départ est la réunion des ensembles de départ des deux correspondances,
- - l’ensemble d’arrivée est la réunion de leurs ensembles d’arrivée,
- - et le graphe est la réunion de leurs graphes.
En d’autres termes, si
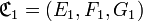 et si
et si 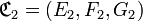 , alors :
, alors :Intersection
L’intersection relationnelle de deux correspondances
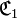 et
et 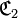 , notée :
, notée :- «
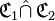 » ( lire « C1 inter C2 » )
» ( lire « C1 inter C2 » )
est la correspondance dont :
- - l’ensemble de départ est l’intersection des ensembles de départ des deux correspondances,
- - l’ensemble d’arrivée est l’intersection de leurs ensembles d’arrivée,
- - et le graphe est l’intersection de leurs graphes.
En d’autres termes, si
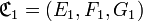 et si
et si 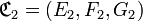 , alors :
, alors :Différence
La différence relationnelle de deux correspondances
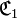 et
et 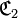 , notée :
, notée :- «
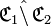 » ( lire « C1 moins C2 » )
» ( lire « C1 moins C2 » )
est la correspondance dont :
- - l’ensemble de départ est l’ensemble de départ de la première correspondance,
- - l’ensemble d’arrivée est l’ensemble d’arrivée de cette correspondance,
- - et le graphe est la différence des graphes des deux correspondances.
En d’autres termes, si
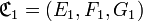 et si
et si 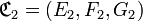 , alors :
, alors :Différence symétrique
La différence symétrique relationnelle de deux correspondances
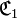 et
et 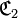 , notée :
, notée :- «
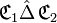 » ( lire « C1 delta C2 » )
» ( lire « C1 delta C2 » )
est la correspondance dont :
- - l’ensemble de départ est la réunion des ensembles de départ des deux correspondances,
- - l’ensemble d’arrivée est la réunion de leurs ensembles d’arrivée,
- - et le graphe est la différence symétrique de leurs graphes.
En d’autres termes, si
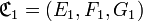 et si
et si 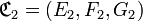 , alors :
, alors :Complémentaire
La correspondance complémentaire relationnelle d’une correspondance
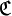 , notée :
, notée :- «
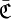 » ( lire « C barre » )
» ( lire « C barre » )
est la correspondance dont :
- - l’ensemble de départ est celui de
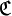 ,
, - - l’ensemble d’arrivée est celui de
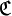 ,
, - - et le graphe est le complémentaire de celui de
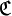 dans le produit cartésien des ensembles de départ et d’arrivée.
dans le produit cartésien des ensembles de départ et d’arrivée.
En d’autres termes, si
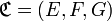 , alors :
, alors :Par exemple, la correspondance complémentaire d’une correspondance vide est une correspondance pleine, et vice versa car :
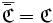 .
.Il ne faut pas confondre les correspondances complémentaires et réciproques. Ainsi, la réciproque d’une correspondance vide est elle-même vide, alors que sa complémentaire est une correspondance pleine.
Remarque importante
En pratique, quand nous rencontrerons une opération ensembliste sur des correspondances, il s’agira en fait d’un abus de langage : par exemple, l’intersection «
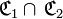 » désignera en fait l’intersection relationnelle «
» désignera en fait l’intersection relationnelle « 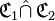 » . Cet abus de langage est sans conséquence puisque les véritables opérations ensemblistes sur les correspondances n’offrent pas d’intérêt. De plus, il rejoint et renforce celui consistant à confondre les correspondances avec leur graphe.
» . Cet abus de langage est sans conséquence puisque les véritables opérations ensemblistes sur les correspondances n’offrent pas d’intérêt. De plus, il rejoint et renforce celui consistant à confondre les correspondances avec leur graphe.Comparaison de correspondances
L’abus de langage précédent s’étend à l'inclusion des correspondances : nous définissons l'inclusion relationnelle de deux correspondances par l’inclusion de leurs ensembles de départ, d’arrivée et graphes respectifs.
En d’autres termes, si
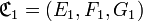 et si
et si 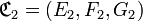 , alors :
, alors :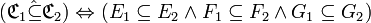 .
.
Là encore, en pratique, nous parlons d'« inclusion » au lieu d'« inclusion relationnelle » et nous notons «
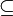 » au lieu de «
» au lieu de « 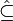 ».
».Restrictions et extensions d’une correspondance
La restriction d’une correspondance à des parties de ses ensembles de départ et d’arrivée est la correspondance dont les ensembles de départ et d’arrivée sont ces parties, et le graphe l’intersection du graphe initial avec le produit cartésien de ces parties.
En d’autres termes, si
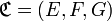 , et si E' et F' sont deux sous-ensembles de E et de F respectivement, alors :
, et si E' et F' sont deux sous-ensembles de E et de F respectivement, alors :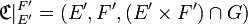 .
.
Il est équivalent d’écrire :
- - la correspondance
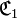 est incluse dans la correspondance
est incluse dans la correspondance 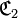 ;
;
- - la correspondance
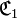 est une restriction de la correspondance
est une restriction de la correspondance 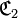 ;
;
- - la correspondance
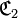 est une extension de la correspondance
est une extension de la correspondance 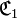 .
.
Si pour deux sous-ensembles donnés des ensembles de départ et d’arrivée d’une correspondance, la restriction obtenue est unique; en revanche, pour deux sur-ensembles donnés des mêmes ensembles de départ et d’arrivée, il est possible a priori de construire plusieurs extensions distinctes, suivant que l’on choisit d’ajouter ou non tel ou tel couple dans le graphe.
Composition des correspondances
Définitions
Le couple composé à partir de deux couples dont la seconde composante du premier est égale à la première composante du second, est le couple dont la première composante est la première composante du premier couple, et la seconde composante la seconde composante du second couple. En d’autres termes :
Le graphe composé de deux graphes est le graphe dont les couples sont tous les couples composés obtenus à partir d’un couple du second graphe et d’un couple du premier graphe.
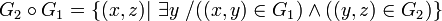 .
.
La correspondance composée de deux correspondances est la correspondance dont :
- - l’ensemble de départ est celui de la seconde correspondance,
- - l’ensemble d’arrivée celui de la première correspondance,
- - et le graphe le composé des deux graphes.
En d’autres termes, si
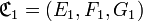 et si
et si 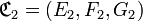 , alors :
, alors :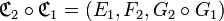 .
.
Propriétés
- La composée de deux correspondances est vide si :
- - l'une des deux correspondances est vide;
- - ou, plus généralement, si l'ensemble d'arrivée de la seconde correspondance n'a pas d'élément commun avec l'ensemble de départ de la première correspondance, c'est-à-dire si :
- Inversement, la composée de deux correspondances est pleine [ssi] les deux correspondances sont pleines et si l'ensemble de départ de la première correspondance se confond avec l'ensemble d'arrivée de la seconde correspondance.
- Il est possible de montrer que, dans la classe des correspondances, la relation «
 » est une loi de composition interne associative :
» est une loi de composition interne associative :
-
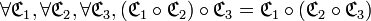 .
.
- En revanche, elle n’est pas commutative, et il est donc vital de respecter l’ordre des compositions! En effet, dans la plupart des cas :
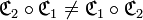 .
.
Composition et Identités
Pour toute correspondance
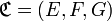 , nous avons d’une part :
, nous avons d’une part : 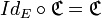 et d’autre part :
et d’autre part : 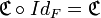 .
.En d’autres termes, les Identités apparaissent comme des « éléments neutres » pour la composition des correspondances. Plus précisément :
- - Id E est neutre à gauche pour les correspondances dont l’ensemble de départ est E ;
- - Id F est neutre à droite pour les correspondances dont l’ensemble d’arrivée est F ;
En particulier, pour toute Identité : Id E
 Id E = Id E.
Id E = Id E.Composition et Réciproque
La composée d’une correspondance par sa réciproque est une relation binaire interne:
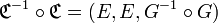 .
.
Plus précisément, cette relation est la relation binaire dans E définie par :
- « x et y sont en relation si et seulement s’ils ont une image commune par
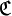 ».
».
Cette relation est évidemment symétrique et transitive, mais elle n'est réflexive, et donc une relation d'équivalence , que si
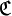 est applicative.
est applicative.Comme toute relation réflexive, elle contient alors l’identité de E :
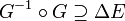 , ou encore :
, ou encore : 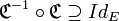 .
.
Nous avons l’inclusion inverse ssi
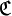 est injective.
est injective.De la même manière, la composée de la réciproque d’une correspondance par celle-ci est la relation binaire dans F définie par :
- « x et y sont en relation si et seulement s’ils ont un antécédent commun par
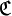 ».
».
Cette relation est une relation d'équivalence ssi
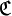 est surjective. Nous avons alors :
est surjective. Nous avons alors :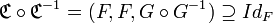 .
.
Cette fois, l’inclusion inverse est obtenue ssi
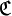 est fonctionnelle.
est fonctionnelle.En résumé, la correspondance réciproque joue le rôle de « symétrique » pour la composition (d’où sa notation). Mais nous n'avons :
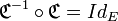 et
et 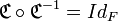
que si
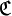 est une bijection.
est une bijection.Réciproque d'une composée
La correspondance réciproque de la composée de deux correspondances est, à l'ordre près, la composée des réciproques de ces deux correspondances :
Puissances de composition
Si
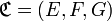 , alors :
, alors :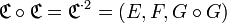
- avec
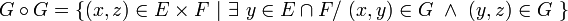
- avec
Plus généralement :
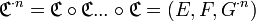
- avec
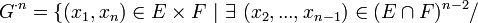
-
- avec
Autres cas de composition importants
- La composée de deux correspondances fonctionnelles est fonctionnelle. Par conséquent, la composée de deux fonctions est encore une fonction.
- La composée de deux correspondances applicatives est applicative. En particulier, la composée de deux applications est encore une application.
- La composée de deux correspondances injectives est injective. En particulier, la composée de deux injections est encore une injection.
- La composée de deux correspondances surjectives est surjective. En particulier, la composée de deux surjections est encore une surjection, et la composée de deux bijections est encore une bijection.
- La composée de deux relations binaires internes est encore une relation binaire interne.
Voir aussi
- Portail des mathématiques
Catégorie : Théorie des ensembles - «
Wikimedia Foundation. 2010.

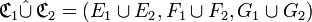
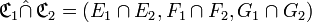
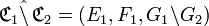
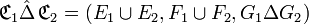
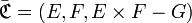
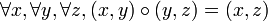
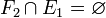
![[ \mathfrak{C}_2 \circ \mathfrak{C}_1 ]^{-1} = ( F_2 , E_1 , [ G_2 \circ G_1 ]^{-1} ) = ( F_2 , E_1 , G_1^{-1} \circ G_2^{-1} ) = \mathfrak{C}_1^{-1} \circ \mathfrak{C}_2^{-1} \,](/pictures/frwiki/100/d69e13d5e22827f6a8382e865e502e47.png)