- Arbre des suffixes
-
Pour les articles homonymes, voir Arbre (homonymie).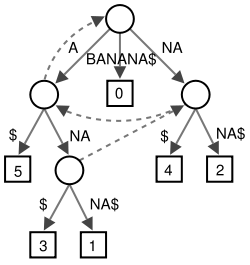
Arbre des suffixes pour le texte
BANANAterminé par$. Les six chemins de la racine à une feuille (représentée par une boîte) correspondent aux six suffixesA$,NA$,ANA$,NANA$,ANANA$etBANANA$. Les nombres dans les boîtes donnent la position de départ du suffixe correspondant. En pointillés sont dessinés les liens suffixes.En informatique, un arbre des suffixes (en anglais suffix tree) est une structure de données arborescente contenant tous les suffixes d'un texte. L'arbre des suffixes est utilisé pour l'indexation de textes.
Sommaire
Définition
Soit un texte dont on veut construire l'arbre des suffixes. L'arbre a les propriétés suivantes :
- Les feuilles de l'arbre contiennent un numéro qui correspond à la position de début du suffixe dans le texte.
- Les branches peuvent être étiquetées de différentes manières :
- par une chaîne de caractères de longueur supérieure ou égale à 1,
- par un couple (p,l) qui correspond à la sous chaîne commençant à la position p, de longueur l, dans le texte.
En général, on termine le texte par un caractère spécial $ (non présent dans le reste du texte), pour éviter que certains suffixes se terminent sur des nœuds de l'arbre.
On peut parler d'arbre compact des suffixes, si :
- chaque nœud a au moins deux fils,
- toutes les étiquettes des branches sortant d'un même nœud commencent par une lettre différente.
Utilisations
Recherche de motifs
L'arbre des suffixes est très utilisé comme structure d'indexation. En effet, il permet, de rechercher un motif M, de longueur m, dans un texte de longueur n en temps O(m). Ainsi, la recherche prend un temps qui dépend uniquement de la longueur du motif.
La recherche de motifs est relativement simple. En partant de la racine de l'arbre, il faut suivre la branche dont l'étiquette commence comme M. En suivant cette branche on arrive alors à un nouveau nœud et on recommence le processus sur la partie restante de M. Le processus est répété jusqu'à :
- ne plus pouvoir descendre dans l'arbre par la lettre lue, il n'y a pas d'occurrence de M dans le texte,
- avoir lu M en entier, on arrive
- sur un nœud de l'arbre ou au milieu d'une branche. Le nombre de feuilles présentes dans le sous arbre correspond au nombre d'occurrences de M dans le texte. De plus chaque feuille contenant la position du début de suffixe, on peut déterminer la position de chacune des occurrences.
- sur une feuille. Il n'y a qu'une seule occurrence de M dans le texte, elle se trouve à la position indiquée par le numéro de la feuille.
Détection de répétitions
Considérons un arbre compact des suffixes. Lorsqu'il y a un nœud, il a au moins deux fils. Cela signifie que la chaîne de caractères qui nous a menée à ce nœud est répétée au moins deux fois dans le texte. Ainsi, en considérant tous les nœuds de l'arbre on peut connaître toutes les répétitions dans le texte.
Construction
La construction de l'arbre des suffixes, sur un texte de longueur n, peut être effectuée en temps O(n)[1],[2], dans un espace O(nlog n) (en pratique de l'ordre de 12n). L'espace utilisé par une telle méthode peut être un problème pour indexer des textes très longs (centaines de Mo à quelques Go). Les principaux algorithmes de construction sont ceux de Weiner, de McCreight et d'Ukkonen. D'autres méthodes existent afin de réduire l'espace mémoire nécessaire aux structures d'indexation. La table des suffixes en est un exemple, bien que l'espace requis puisse être trop important (de l'ordre de 4n). De nouvelles méthodes consistant à compacter ou compresser les structures font leur apparition et sont encore l'objet de recherches de nos jours. Des chercheurs de l'université d'Helsinki ont mis au point un outil permettant de naviguer dans l'arbre des suffixes d'un génome humain[3].
Voir aussi
Notes et références
- Edward M. McCreight, « A Space-Economical Suffix Tree Construction Algorithm », dans Journal of the ACM, vol. 23, no 2, 1976, p. 262--272 [texte intégral]
- Esko Ukkonen, « On-line construction of suffix trees », dans Algorithmica, vol. 14, no 3, 1995, p. 249--260 [texte intégral]
- SuDS Genome Browser
Liens externes
- Construction d'Arbres de Suffixes Introduction à la construction et à l'utilisation d'arbres de suffixes, présentation et comparaison des algorithmes de Ukkonen et de Hunt avec l'approche TDD.
Catégories :- Arbre (structure de données)
- Informatique théorique
- Algorithme sur les chaînes de caractères
Wikimedia Foundation. 2010.
