Nombres étrangers

En mathématiques, on dit que des entiers a et b sont premiers entre eux, ou que a est premier avec b, s'ils n'ont aucun facteur premier en commun ; en d'autres termes, s'ils n'ont aucun diviseur autre que 1 et -1 en commun. De manière équivalente, ils sont premiers entre eux si et seulement si leur plus grand commun diviseur est égal à 1.

Par exemple, 6 et 35 sont premiers entre eux, mais 6 et 27 ne le sont pas parce qu'ils sont tous les deux divisibles par 3. 1 est premier avec tout entier ; 0 n'est pas premier.

Un moyen rapide pour déterminer si deux nombres entiers sont premiers entre eux est l'algorithme d'Euclide.

Sommaire 1 Propriétés 1.1 Théorème de Bachet de Méziriac-Bezout 1.2 Théorème de Gauss 1.3 Extension à n nombres 2 Généralisation 3 Voir aussi

Propriétés

Théorème de Bachet de Méziriac-Bezout

Les entiers relatifs a et b sont dits premiers entre eux si et seulement s’il existe des entiers relatifs x et y tels que ax + by = 1 (voir Théorème de Bachet-Bézout).

De façon équivalente, b a un inverse pour la multiplication modulo a : il existe un nombre entier y tel que by ≡ 1 (mod a).

Théorème de Gauss

Si a et b sont premiers entre eux et a divise un produit bc, alors a divise c.

Si a et b sont premiers entre eux et bx ≡ by (mod a), alors x ≡ y (mod a). En d'autres termes: b est simplifiable dans l'anneau Z/aZ des entiers modulo a.

Les deux entiers a et b sont premiers entre eux si et seulement si le point de coordonnées (a,b) dans un repère cartésien est « visible » de l'origine (0,0), dans le sens où il n'y a pas de point de coordonnées entières entre l'origine et (a,b).

La probabilité pour que deux nombres entiers choisis au hasard soient premiers entre eux est égale à 6/π² (Voir Pi).

Deux entiers naturels a et b sont premiers entre eux si et seulement si les nombres 2^a-1 et 2^b-1 sont premiers entre eux.

Extension à n nombres

n nombres A1,…,An sont premiers entre eux si leur plus grand commun diviseur vaut 1. (on a vu que le PGCD peut s'étendre à un nombre arbitraire d'entiers).

Ils sont premiers entre eux deux à deux si pour tout i différent de j, Ai et Aj sont premiers entre eux.

Note: la présence d'un couple de nombre premiers entre eux parmi n nombres est une condition suffisante, mais non nécessaire, pour que ces n nombres soient premiers entre eux.

Exemple: 6, 14 et 21 sont premiers entre eux, mais aucun couple extrait de ce triplet n'est formé de deux nombres premiers entre eux.

Généralisation

Des idéaux I et J d'un anneau commutatif A sont dits premiers entre eux si I + J = A. Cela généralise l'identité de Bézout. Si I et J sont premiers entre eux, alors IJ = I∩J ; de plus, si K est un troisième idéal tel que I contient JK, alors I contient K.

Avec cette définition, des idéaux principaux (a) et (b) dans l'anneau des nombres entiers relatifs 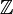sont premiers entre eux si et seulement si a et b sont premiers entre eux.

Voir aussi

• Plus grand commun diviseur
• Livre VII des Éléments d'Euclide

• Portail des mathématiques