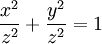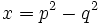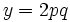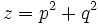Nombres pythagoriciens

Nombres pythagoriciens

Triplet pythagoricien

Un triplet pythagoricien est un triplet d'entiers naturels non nuls (x; y; z) vérifiant la relation de Pythagore :

x2 + y2 = z2

Sommaire

Triplets primitifs

Nous dirons qu'un triplet pythagoricien est primitif si les trois naturels x, y, z sont premiers entre eux.

Remarque - Cette définition équivaut à l'affirmation : deux des naturels x, y, z sont premiers entre eux (immédiat puisqu'un diviseur premier commun de deux des nombres divisera le troisième).

Il est évident qu'on obtiendra tous les triplets pythagoriciens par multiplication des trois nombres par un naturel non nul. On peut donc se contenter d'obtenir les triplets primitifs.

Remarquons que si on divise par z2, on obtient :

\frac{x^2}{z^2} + \frac{y^2}{z^2} = 1

C’est-à-dire que les triplets pythagoriciens permettent de trouver les points à coordonnées rationnelles donnés par (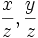\frac{x}{z},\frac{y}{z}) sur le cercle unité.

Lemme préliminaire

Si (x, y, z) est un triplet pythagoricien primitif, alors x et y sont de parités différentes.

En effet x et y ne peuvent être tous deux pairs en vertu de la remarque ci-dessus. D'autre part, s'ils étaient tous deux impairs en posant x = 2s + 1 et y = 2t + 1 on voit que z2 = x2 + y2 serait de la forme 4m + 2, ce qui est impossible puisqu'un tel naturel ne peut être un carré (un naturel pair qui est un carré ne peut être que le carré d'un nombre pair 2q et ce carré 4q2 est multiple de 4).

Comment en obtenir ?

Prenons x un entier naturel supérieur ou égal à 3, dont on cherche un triplet pythagoricien primitif (x, y, z) tel que x² + y² = z², avec x < y.

Voici comment en obtenir un :

1er cas : x est impair.

y est alors égal à (x² - 1)/2 ;

et z est égal à (x² + 1)/2 ; c'est-à-dire y + 1.

2e cas : x est pair (et divisible par 4, sinon le triplet n'est pas primitif).

y vaut alors (x/2)² - 1 ;

et z vaut (x/2)² + 1 ; soit y + 2.

Remarque : avec cette méthode, certains triplets pythagoriciens ne peuvent pas être obtenus, comme par exemple (20, 21, 29).

Théorème fondamental

Il y a équivalence entre

  • (i) 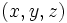\quad (x,y,z) est un triplet pythagoricien primitif avec x impair.
  • (ii) Il existe 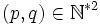(p,q) \in \mathbb N^{*2} avec p > q , p et q premiers entre eux et de parités différentes tels que
    • \quad x=p^2-q^2
    • \quad y=2pq
    • \quad z=p^2+q^2

Démonstration

  • (i) 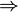\Rightarrow (ii)

y étant pair, posons y = 2u (u 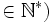\in \mathbb N^*). On a donc z2 - x2 = 4u2, soit (z + x)(z - x ) = 4u2.

Comme z + x et z - x sont pairs (x et z impairs), posons z + x = 2s et z - x = 2t (s et t 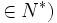\in N^*). Il vient alors

x = s - t, z = s + t, st = u2.

s et t sont premiers entre eux. En effet tout diviseur premier commun de s et t diviserait s + t = z, s - t = x et 2√st = y, ce qui est impossible (cf. remarque sur les triplets primitifs). Chaque diviseur premier de st = u2 ne peut donc diviser à la fois s et t et, comme u2 est un carré, l'exposant de ce diviseur premier est pair dans celui des 2 nombres s et t où ce diviseur premier figure. Il en résulte que s et t sont des carrés de naturels (non nuls) puisque chacun de leurs diviseurs premiers a un exposant pair. On peut donc poser s = p2 et t = q2.

On a donc bien x = p2 - q2 et z = p2 + q2. De plus st = u2, soit p2q2 = u2 et donc u = pq d'où y = 2pq. Comme s et t sont premiers entre eux, il en est de même de p et q. Comme x > 0 on a p > q. Enfin p et q ne peuvent être de même parité puisque alors x = p2 - q2 serait pair.


  • (ii) 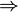\Rightarrow (i)

(ii) entraîne immédiatement par un simple calcul que x2 + y2 = z2. D'autre part, comme p et q sont de parités différentes, x est nécessairement impair. Si x et z avaient un diviseur premier commun, ce diviseur diviserait z + x et z - x, soit 2p2 et 2q2. Comme ce diviseur premier ne peut être 2 (x impair), il diviserait p2 et q2 et donc p et q, ce qui est impossible puisque p et q sont premiers entre eux.

CQFD

Exemples de triplets primitifs

( 3, 4, 5) (20, 21, 29) (11, 60, 61) (13, 84, 85)
( 5, 12, 13) (12, 35, 37) (16, 63, 65) (36, 77, 85)
( 8, 15, 17) ( 9, 40, 41) (33, 56, 65) (39, 80, 89)
(7, 24, 25) (28, 45, 53) (48, 55, 73) (65, 72, 97)

Faits intéressants

Dans un triplet pythagoricien primitif où a et b sont les cathètes et c est l'hypoténuse, a étant impair et b pair (voir lemme préliminaire):

c est toujours impair.

c - b est un carré parfait.

c + b est un carré parfait.

(c + a) / 2 est un carré parfait.

(c - a) / 2 est un carré parfait.

Soit a soit b est un multiple de 3.

b est un multiple de 4.

Soit a soit b soit c est un multiple de 5.

Le produit ab est un multiple de 12.

Soit a soit b soit a + b soit b - a est un multiple de 7.


Par exemple, dans le triplet pythagoricien 65 - 72 - 97, où a = 65, b = 72 et c = 97:

97 est impair,

97 - 72 = 25, qui est un carré parfait (5 x 5),

97 + 72 = 169, qui est aussi un carré parfait (13 x 13),

(97 + 65) / 2 = 81, qui est un carré parfait (9 x 9),

(97 - 65) / 2 = 16, qui est aussi un carré parfait (4 x 4),

72 est un multiple de 3,

72 est un multiple de 4,

65 est un multiple de 5,

65 * 72 = 4680 est un multiple de 12,

72 - 65 = 7 , qui est un multiple de 7.


Information trouvée dans le livre Math Power, par Robert Stanton, Éditions KAPLAN.

Voir aussi

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Triplet pythagoricien ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Nombres pythagoriciens de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • NOMBRES (THÉORIE DES) — DANS la plupart des civilisations parvenues au stade de l’écriture, les nombres entiers ont, dès l’origine, été liés à des pratiques religieuses ou magiques, et leurs propriétés ont exercé une sorte de fascination sur les esprits, qui est loin… …   Encyclopédie Universelle

  • NOMBRES (SYMBOLIQUE DES) — NOMBRES SYMBOLIQUE DES De nombreuses études d’ethnologie comme de philosophie comparée, d’histoire des religions comme de psychologie des profondeurs ont montré que la pensée dite «sauvage» comme la connaissance symbolique présentent une… …   Encyclopédie Universelle

  • Nombres premiers — Nombre premier 7 est un nombre premier car il admet exactement deux diviseurs positifs …   Wikipédia en Français

  • Nombres premiers somme de 2 carrés — Théorème des deux carrés de Fermat Pierre Fermat En mathématiques, le théorème des deux carrés de Fermat énonce les conditions pour qu’un nombre entier soit la somme de deux carrés parfaits (c est à dire de deux carrés d’entiers) et précise de… …   Wikipédia en Français

  • Nombres Amicaux — Nombre amical En mathématiques et plus précisément en arithmétique modulaire, deux nombres entiers n et m sont dits amicaux ou aimables ou amiables si où est la fonction donnant la somme des diviseurs entiers positifs de , incluant lui même.… …   Wikipédia en Français

  • Nombres amicaux — Nombre amical En mathématiques et plus précisément en arithmétique modulaire, deux nombres entiers n et m sont dits amicaux ou aimables ou amiables si où est la fonction donnant la somme des diviseurs entiers positifs de , incluant lui même.… …   Wikipédia en Français

  • Nombres amis — Nombre amical En mathématiques et plus précisément en arithmétique modulaire, deux nombres entiers n et m sont dits amicaux ou aimables ou amiables si où est la fonction donnant la somme des diviseurs entiers positifs de , incluant lui même.… …   Wikipédia en Français

  • Symbolique des nombres — Symbolisme des nombres Le symbolisme des nombres concerne les nombres en tant que symboles, dans leur puissance à représenter analogiquement, à être interprétés, à porter sens et valeurs (en plus de l aspect mathématique). On entre dans l étude… …   Wikipédia en Français

  • Symbolisme des nombres — Le symbolisme des nombres concerne les nombres en tant que symboles, dans leur puissance à représenter analogiquement, à être interprétés, à porter sens et valeurs (en plus de l aspect mathématique). On entre dans l étude des nombres en tant que… …   Wikipédia en Français

  • Caractérisation des nombres premiers — Nombre premier 7 est un nombre premier car il admet exactement deux diviseurs positifs …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”