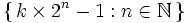Nombre de riesel

Nombre de riesel

Nombre de Riesel

Un nombre de Riesel est, en mathématiques un entier naturel impair k pour lequel les entiers de la forme k×2n-1 sont tous composés.

Sommaire

Définition

Soit 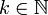k \in \mathbb N. k est un nombre de Riesel si tous les éléments de l'ensemble suivant sont composés :

\left\{\,k \times 2^n - 1 : n \in\mathbb{N}\,\right\}

Propriétés

En 1956, Hans Riesel a montré qu'il existait une infinité d'entiers de la sorte. Il a montré également que le nombre 509 203 possédait cette propriété, ainsi que toute somme de 509 203 et d'un multiple de 11 184 810.

On peut montrer qu'un nombre est de Riesel en déterminant son ensemble de couverture. Un ensemble de couverture est un ensemble de nombres premiers qui divisent tous les membres d'une suite. Les seuls nombres de Riesel connus en dessous d'un million ont les ensembles de couverture suivant :

  • 509203 : {3, 5, 7, 13, 17, 241}
  • 762701 : {3, 5, 7, 13, 17, 241}
  • 777149 : {3, 5, 7, 13, 19, 37, 73}
  • 790841 : {3, 5, 7, 13, 19, 37, 73}
  • 992077 : {3, 5, 7, 13, 17, 241}

Problème de Riesel

Le problème de Riesel consiste en la détermination du plus petit nombre de Riesel. Actuellement (juin 2008), on conjecture que 509 203 est le plus petit nombre de Riesel. Cependant, 64 nombres inférieurs ont pour l'instant donné des nombres composés pour toutes les valeurs de n testées :

2293, 9221, 23669, 31859, 38473, 40597, 46663, 65531, 67117, 74699, 81041, 93839, 97139, 107347, 113983, 121889, 123547, 129007, 141941, 143047, 146561, 161669, 162941, 191249, 192971, 206039, 206231, 215443, 226153, 234343, 245561, 250027, 252191, 273809, 304207, 315929, 319511, 324011, 325123, 327671, 336839, 342847, 344759, 353159, 362609, 363343, 364903, 365159, 368411, 371893, 384539, 386801, 397027, 398023, 402539, 409753, 415267, 428639, 444637, 470173, 474491, 477583, 485557, 494743, 502573.

Voir aussi

Liens internes

Liens externes

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Nombre de Riesel ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Nombre de riesel de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

  • Nombre De Riesel — Un nombre de Riesel est, en mathématiques un entier naturel impair k pour lequel les entiers de la forme k×2n 1 sont tous composés. Sommaire 1 Définition 2 Propriétés 3 Problème de Riesel …   Wikipédia en Français

  • Nombre de Riesel — Un nombre de Riesel est, en mathématiques un entier naturel impair k pour lequel les entiers de la forme k×2n 1 sont tous composés. Sommaire 1 Définition 2 Propriétés 3 Problème de Riesel …   Wikipédia en Français

  • Nombre De Sierpinski — Nombre de Sierpiński En mathématiques, un nombre de Sierpinski est un nombre positif, impair k tel que les entiers de la forme sont composés (c.a.d. non premier) pour tous les nombres naturels n. En 1960 Wacław Sierpiński montra qu il existe une… …   Wikipédia en Français

  • Nombre De Woodall — En mathématiques, un nombre de Woodall ou nombre de Riesel est un entier naturel de la forme (écrit ). Les nombres de Woodall ont été étudiés en premier par A. J. C. Cunningham et H. J. Woodall en 1917, inspirés par l étude précédente de James… …   Wikipédia en Français

  • Nombre de Sierpinski — Nombre de Sierpiński En mathématiques, un nombre de Sierpinski est un nombre positif, impair k tel que les entiers de la forme sont composés (c.a.d. non premier) pour tous les nombres naturels n. En 1960 Wacław Sierpiński montra qu il existe une… …   Wikipédia en Français

  • Nombre de sierpinski — Nombre de Sierpiński En mathématiques, un nombre de Sierpinski est un nombre positif, impair k tel que les entiers de la forme sont composés (c.a.d. non premier) pour tous les nombres naturels n. En 1960 Wacław Sierpiński montra qu il existe une… …   Wikipédia en Français

  • Nombre de woodall — En mathématiques, un nombre de Woodall ou nombre de Riesel est un entier naturel de la forme (écrit ). Les nombres de Woodall ont été étudiés en premier par A. J. C. Cunningham et H. J. Woodall en 1917, inspirés par l étude précédente de James… …   Wikipédia en Français

  • Nombre de Sierpiński — En mathématiques, un nombre de Sierpiński est un nombre positif, impair k tel que les entiers N de la forme sont composés (c est à dire non premiers) pour tous les nombres naturels n. En 1960, Wacław Sierpiński montra qu il existe une infinité de …   Wikipédia en Français

  • Nombre de Woodall — En mathématiques, un nombre de Woodall ou nombre de Riesel est un entier naturel de la forme (écrit ). Les nombres de Woodall ont été étudiés en premier par A. J. C. Cunningham et H. J. Woodall en 1917, inspirés par l étude précédente de James… …   Wikipédia en Français

  • Nombre Premier De Mersenne — Marin Mersenne En mathématiques et plus précisément en arithmétique modulaire, un nombre premier de Mersenne est un nombre premier s écrivant sous la forme 2p 1, p étant premier. Ces nombres premiers doivent leur nom à un érudit et mathématicien… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”