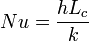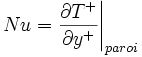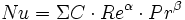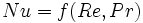Nombre de nusselt

Nombre de Nusselt

Le nombre de Nusselt (Nu) est un nombre adimensionnel utilisé dans les opérations de transfert thermique. Il représente le rapport entre le transfert thermique total et le transfert par conduction. Si la conduction est seule responsable du transfert de chaleur, alors le nombre de Nusselt vaudra 1.

On le définit de la manière suivante:

$Nu = \frac{h L_c}{k}$

avec

h - coefficient de transfert thermique
L_c - longueur caractéristique
k - conductivité thermique du fluide

La longueur caractéristique dépend de la géométrie en présence. Dans le cas d'un écoulement dans une conduite, on prendra le diamètre de la canalisation, ou le diamètre hydraulique si la conduite n'a pas une section circulaire. Dans le cas d'une plaque plane, on prendra la longueur de la plaque, ou l'abscisse à compter du bord d'attaque de la plaque. Comme tout nombre sans dimension, la valeur du nombre de Nusselt dépend fortement des grandeurs de référence que l'on choisit, et de la signification physique que l'on entend lui donner (locale ou globale par exemple). Il est notamment important de savoir, lors de l'utilisation d'une corrélation, si le coefficient de convection h a été défini par rapport à une température de référence fixe, ou à une température de mélange locale.

Interprétation du nombre de Nusselt

Le nombre de Nusselt local est égal au gradient de température adimensionné à la paroi.

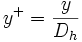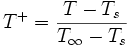En posant $y^+ = {y \over D_h}$ et $T^+ = {{T-T_s} \over {T_{\infty}-T_s}}$ , on obtient à partir de l'équation de définition du coefficient de transfert :

$Nu=\frac{\partial T^+}{\partial y^+}\Bigg|_{paroi}$

Nombre de Nusselt local ou moyen

Utilisation en transfert thermique

L'application du théorème de Buckingham à un problème de convection forcée fait apparaître trois groupements ou nombres sans dimension en relation sous la forme suivante :

$Nu = \Sigma C \cdot Re^\alpha \cdot Pr^\beta$

avec :

Re le nombre de Reynolds
Pr le nombre de Prandtl

Cette somme représente une fonction quelconque des deux variables qui ne peut être précisée que par l'expérience :

$Nu = f(Re,Pr)\,$

Ici, l'expérience montre qu'une fonction monôme est généralement adéquate.

L'objectif est, en général, de calculer le Nusselt afin d'en déduire le coefficient de transfert

Principaux résultats et corrélations

Convection naturelle sur une plaque plane

$N u = 0.59(P r . G r) 0.25$ pour $104 < (P r . G r) < 10 9$

$N u = 0.13(P r . G r) 0.33$ pour $(P r . G r) > 10 9$

$G r$ : nombre de Grashof ; $P r$ : nombre de Prandtl

Convection forcée dans une conduite en régime laminaire

Si le tube est long $(L / D > 0.1 R e . P r)$ :

Température de paroi uniforme : $N u = 3.66$

Flux de chaleur pariétal uniforme : $N u = 4.36$

Ces deux résultats ont été obtenus analytiquement.

Si le tube est court, i.e, le régime thermique n'est pas établi, on peut utiliser la corrélation de Sider et Tates :

$N u = 1.86(R e . P r . D / L) 0.33 (μ / μ p) 0.14$

Applicable pour : $L / D < 0.1 R e . P r$ ; $100 < R e < 2100$ ; $0.6 < P r < 100$

Convection forcée dans une conduite en régime turbulent

Conduites lisses : Corrélation de Dittus-Boelter : $N u = 0.0243 R e 0.8 . P r n$

Echauffement : n=0.4 ; Refroidissement : n=0.3

Applicable pour : $L / D > 60$ ; $104 < R e < 1.2.10 5$ ; $0.7 < P r < 120$

Corrélation de Colburn : $N u = 0.023 R e 0.8 P r 1 / 3$ Viscosité évaluée à la température de film (nécessite un calcul itératif)

Voir aussi

Portail de la physique

Ce document provient de « Nombre de Nusselt ».

Catégorie : Nombre adimensionnel utilisé en thermodynamique

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Nombre de nusselt de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Nombre De Nusselt — Le nombre de Nusselt (Nu) est un nombre adimensionnel utilisé dans les opérations de transfert thermique. Il représente le rapport entre le transfert thermique total et le transfert par conduction. Si la conduction est seule responsable du… … Wikipédia en Français
Nombre de Nusselt — Le nombre de Nusselt (Nu) est un nombre adimensionnel utilisé dans les opérations de transfert thermique. Il représente le rapport entre le transfert thermique par convection et le transfert par conduction. Si la conduction et la convection sont… … Wikipédia en Français
nombre de Nusselt — Nuselto skaičius statusas T sritis Energetika apibrėžtis Skaičius, apibūdinantis šilumos mainų intensyvumo padidėjimą dėl konvekcijos, palyginti su grynuoju šilumos laidumu. atitikmenys: angl. Nusselt number vok. Nusselt Zahl, f rus. число… … Aiškinamasis šiluminės ir branduolinės technikos terminų žodynas
Nombre De Rayleigh — Le nombre de Rayleigh (Ra) est un nombre sans dimension utilisé en mécanique des fluides et caractérisant le transfert de chaleur au sein d un fluide : inférieur à une valeur critique de 2000, le transfert s opère essentiellement par… … Wikipédia en Français
Nombre de rayleigh — Le nombre de Rayleigh (Ra) est un nombre sans dimension utilisé en mécanique des fluides et caractérisant le transfert de chaleur au sein d un fluide : inférieur à une valeur critique de 2000, le transfert s opère essentiellement par… … Wikipédia en Français
Nombre De Sherwood — Le nombre de Sherwood (Sh) est un nombre sans dimension utilisé dans les opérations de transfert de masse. Il représente le rapport entre le transfert total de masse et le transfert par diffusion. Si la diffusion est seule responsable du… … Wikipédia en Français
Nombre de sherwood — Le nombre de Sherwood (Sh) est un nombre sans dimension utilisé dans les opérations de transfert de masse. Il représente le rapport entre le transfert total de masse et le transfert par diffusion. Si la diffusion est seule responsable du… … Wikipédia en Français
Nusselt — Ernst Kraft Wilhelm Nusselt Ernst Kraft Wilhelm Nusselt (Nuremberg, 25 novembre 1882 Munich, 1er septembre 1957) est un physicien allemand. C est un pionnier dans l étude de transfert par convection. Son nom reste attaché au nombre … Wikipédia en Français
Nusselt number — Nuselto skaičius statusas T sritis Energetika apibrėžtis Skaičius, apibūdinantis šilumos mainų intensyvumo padidėjimą dėl konvekcijos, palyginti su grynuoju šilumos laidumu. atitikmenys: angl. Nusselt number vok. Nusselt Zahl, f rus. число… … Aiškinamasis šiluminės ir branduolinės technikos terminų žodynas
Nusselt-Zahl — Nuselto skaičius statusas T sritis Energetika apibrėžtis Skaičius, apibūdinantis šilumos mainų intensyvumo padidėjimą dėl konvekcijos, palyginti su grynuoju šilumos laidumu. atitikmenys: angl. Nusselt number vok. Nusselt Zahl, f rus. число… … Aiškinamasis šiluminės ir branduolinės technikos terminų žodynas

Dictionnaires et Encyclopédies sur 'Academic'

Nombre de nusselt

Nombre de Nusselt

Sommaire

Interprétation du nombre de Nusselt

Nombre de Nusselt local ou moyen

Utilisation en transfert thermique

Principaux résultats et corrélations

Convection naturelle sur une plaque plane

Convection forcée dans une conduite en régime laminaire

Convection forcée dans une conduite en régime turbulent

Voir aussi

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Nombre de nusselt

Nombre de Nusselt

Sommaire

Interprétation du nombre de Nusselt

Nombre de Nusselt local ou moyen

Utilisation en transfert thermique

Principaux résultats et corrélations

Convection naturelle sur une plaque plane

Convection forcée dans une conduite en régime laminaire

Convection forcée dans une conduite en régime turbulent

Voir aussi

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link