- Negation by failure
-
Négation par l'échec
La négation par l'échec (en anglais NAF pour negation as failure, ou NBF pour negation by failure) est une règle d'inférence non monotone en programmation logique, utilisée pour la dérivation de
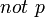à partir de l'échec de la dérivation de p. C'est une caractéristique importante de la programmation logique depuis les origines de Planner et de Prolog. En Prolog, la négation par l'échec est habituellement implémentée en utilisant les fonctionnalités non logiques du langage.En Prolog pur, les littéraux de négation par l'échec (littéraux négatifs) de la forme
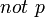peuvent apparaître dans le corps des clauses et peuvent être utilisés pour dériver d'autres littéraux négatifs. Par exemple, si l'on considère uniquement les quatre clauses suivantes :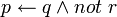
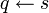
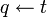
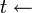
La négation par l'échec dérive
, 
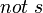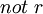et p.Sommaire
Sémantique par complétion
La sémantique de la négation par l'échec est restée un problème ouvert jusqu'à ce que Keith Clark montre en 1978[1] qu'elle était correcte par rapport à la complétion du programme logique où, en gros, « seulement » et
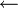sont interprétés comme « si et seulement si », abrégé en « ssi » et noté 
.Par exemple, la complétion des quatre clauses précédentes est :
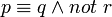
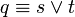
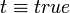
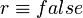
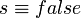
La règle d'inférence de la négation par l'échec simule un raisonnement avec une complétion explicite, où la négation est appliquée aux deux côtés de l'équivalence et où la négation de la partie droite est distribuée sur les formules atomiques. Par exemple, pour montrer
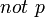, la négation par l'échec simule un raisonnement avec les équivalences suivantes :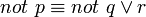
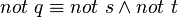
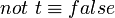
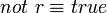
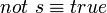
Dans le cas non propositionnel, il faut étendre la complétion avec des axiomes d'égalité, pour formaliser l'hypothèse que des entités avec des noms différents sont elles-mêmes distinctes. La négation par l'échec simule ceci par l'échec de l'unification. Par exemple, si l'on considère uniquement les deux clauses suivantes :
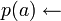
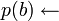
On dérive, avec la négation par l'échec,
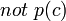.La complétion du programme est :
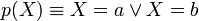
étendue avec les axiomes d'unicité des noms et de fermeture du domaine.
La sémantique par complétion est étroitement liée à la notion de circonscription et à l'hypothèse du monde fermé.
Sémantique auto-épistémique
La sémantique par complétion justifie l'interprétation du résultat
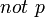d'une inférence en négation par l'échec comme la négation classique 
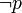de p. Cependant, Michael Gelfond a montré en 1987[2] qu'il était également possible d'interpréter 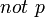de manière littérale comme « p ne peut pas être montré », « p n'est pas connu » ou « p n'est pas cru », comme en logique auto-épistémique. L'interprétation auto-épistémique a été développée en 1988 par Gelfond et Lifschitz[3], et constitue la base de l'answer set programming.La sémantique auto-épistémique d'un programme Prolog pur P avec la négation par l'échec sur des littéraux est obtenue en « étendant » P avec un ensemble Δ de littéraux négatifs (au sens de la négation par l'échec) exempts de variable libres tel que Δ soit stable au sens où :
Δ = {
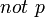| P ∪ Δ n'implique pas p}En d'autres termes, un ensemble d'hypothèses Δ sur ce qui ne peut pas être démontré est stable si et seulement si Δ est l'ensemble de toutes les formules qui ne peuvent véritablement pas être montrées à partir du programme P étendu à l'aide de Δ. Ici, à cause de la syntaxe simple des programmes en Prolog pur, l'implication peut être comprise simplement comme la dérivabilité à l'aide du modus ponens et de la substitution uniforme, à l'exception de tout autre règle.
Un programme peut avoir zéro, une ou plusieurs extensions stables. Par exemple, le programme suivant n'a aucune extension stable :
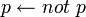
Celui-ci a exactement une extension stable Δ = {
}
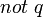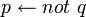
Ce troisième programme a deux extensions stables Δ1 = {
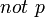} et Δ2 = {}.
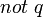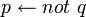
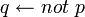
L'interprétation auto-épistémique de la négation par l'échec peut être combinée avec la négation classique, comme en programmation logique étendue et en answer set programming. En combinant les deux négations, on peut par exemple exprimer l'hypothèse du monde fermé :
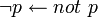
Ou encore la valeur par défaut d'une proposition :
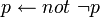
Notes et références de l'article
- ↑ (en)Keith Clark, "Negation as Failure", Readings in Nonmonotonic Reasoning, Morgan Kaufmann Publishers, 1978, pages 311-325, abstract en ligne.
- ↑ (en) M. Gelfond, "On Stratified Autoepistemic Theories", AAAI-87 Sixth National Conference on Artificial Intelligence, 1987, pages 207-211, lire en ligne.
- ↑ (en) M. Gelfond and V. Lifschitz, "The Stable Model Semantics for Logic Programming", 5th International Conference and Symposium on Logic Programming, R. Kowalski et K. Bowen (éditeurs), MIT Press, 1988, pages 1070-1080, lire en ligne.
- (en) Cet article est partiellement ou en totalité issu d’une traduction de l’article de Wikipédia en anglais intitulé « Negation as failure ».
Voir aussi
Articles connexes
Liens et documents externes
- (en)Rapport de l'atelier W3C sur les langages de règles pour l'interopérabilité, incluant des notes sur la négation par l'échec et la négation par l'échec avec portée (scoped negation as failure).
Portail de la logique
Catégorie : Logique
Wikimedia Foundation. 2010.
