Appui gravitationnel

L'appui gravitationnel ou appui gravitationnel, dans le domaine de la mécanique spatiale, est l'utilisation volontaire de l'attraction d'un corps céleste (planète, lune) pour modifier en direction et en vitesse la trajectoire d'un engin spatial (sonde spatiale, satellite artificiel,...). L'objectif est d'utiliser ce phénomène pour économiser le carburant qui aurait du être consommé par le moteur-fusée du véhicule pour obtenir le même résultat. Toutes les sondes spatiales à destination des corps célestes éloignées de la Terre ont recours à cette méthode.

Explication

Dans un premier temps, l'engin spatial s'approche de la planète et finit par rentrer dans sa zone d'influence (il entre dans sa sphère de Hill). Le champ gravitationnel attire de plus en plus l'engin spatial qui voit sa vitesse augmenter : il « tombe » vers la planète et donc accélère. La trajectoire de l'engin a été établie de manière à éviter une collision avec la planète choisie. Il dépasse donc la planète sain et sauf et sort progressivement du champ gravitationnel de celle-ci, en perdant petit à petit de la vitesse. À la fin du survol (lorsqu'il sort de la sphère de Hill), l'engin spatial a perdu autant de vitesse pendant la phase de sortie qu'il en a gagné pendant la phase d'entrée. Vous vous demandez sans doute l'intérêt d'une telle manœuvre qui n'a apparemment servi à rien. Pourtant sa vitesse a considérablement changé, en grandeur et en direction.

Du point de vue de la planète, l'engin suit une trajectoire hyperbolique, tracée de son point d'entrée dans la sphère de Hill de la planète jusqu'à sa sortie. À ces points, la vitesse de l'engin est la même, mais son orientation est différente. Du point de vue du Soleil, l'orientation et la magnitude de la vitesse de l'engin ont changé. Ceci permet soit d'envoyer l'engin plus loin du Soleil (il emprunte alors de l'énergie et du moment angulaire à la planète), ou au contraire de diminuer son orbite (l'engin donne énergie et moment angulaire à la planète). C'est précisément par ce mécanisme que les planètes peuvent capturer des comètes ou éjecter des astéroïdes du système solaire.

Illustrations de l'utilisation de l'assistance gravitationnelle

Une sonde spatiale frôle une planète selon deux scénarios. La courbe rouge dans le graphique représente l'évolution de la vitesse de la sonde spatiale dans le temps.

Trajectoire permettant d'augmenter la vitesse

Trajectoire permettant de diminuer la vitesse

Exemple

Prenons comme exemple Voyager 2, qui a fait le tour des planètes géantes. Le vaisseau spatial a été lancé sur une orbite standard de transfert de Hohmann vers Jupiter. Si Jupiter n'avait pas été là au moment de l'arrivée du vaisseau spatial, celui-ci aurait continué sur son orbite et serait revenu vers la Terre.

Cependant, l'arrivée de la sonde spatiale a été soigneusement calculée de sorte qu'elle passe derrière Jupiter dans son orbite autour du Soleil. Quand la sonde est arrivée, elle est "tombée" vers Jupiter, sous l'influence de son champ de gravité. L'orbite était néanmoins faite pour que la sonde passe près de Jupiter mais ne s'écrase pas dessus. Après s'être approché très près de Jupiter la sonde s'est alors éloignée de la planète. Pendant cette phase d'éloignement, elle a ralenti par rapport à Jupiter. En effet elle "s'élevait" par rapport à Jupiter, et donc ralentissait comme elle avait accéléré quand elle était tombée vers lui. Dans le cas des trajectoires dans l'espace, il y a conservation de l'énergie : la sonde a donc quitté Jupiter (on entend par là quitter la zone d'influence gravitationnelle de Jupiter) avec la même énergie que quand elle y était arrivée. Pour l'instant on ne comprend pas bien ce que l'on a gagné, car il n'y a pas eu de changement d'énergie pour la sonde.

Cependant, dans le référentiel héliocentrique, l'énergie de la sonde a bien changé. En effet son vecteur vitesse a tourné dans le référentiel de Jupiter, grâce la gravitation. Et le fait qu'il ait tourné, fait qu'à la sortie de la sphère d'influence de Jupiter, la somme entre le vecteur vitesse de la sonde dans le référentiel de Jupiter et le vecteur vitesse de Jupiter autour du soleil (somme qui est donc le vecteur vitesse de la sonde autour du soleil) est plus importante qu'avant car l'angle entre les deux vecteurs est plus faible.

Remarquons aussi que la force de gravité est réciproque : si la sonde a bien été accélérée par Jupiter, alors Jupiter a aussi été ralentie par la sonde. Néanmoins, ce ralentissement de Jupiter est tout à fait infime puisque dépendant du rapport entre la masse de la sonde (moins d'une tonne, soit 1×10³ kg) et la masse de Jupiter (environ 2×10²⁷ kg). On pourrait envoyer des milliers et des milliers de sondes de cette façon que Jupiter ne serait nullement perturbée dans sa course autour du Soleil...

Cette technique a été répétée ensuite à l'approche de Saturne et Uranus.

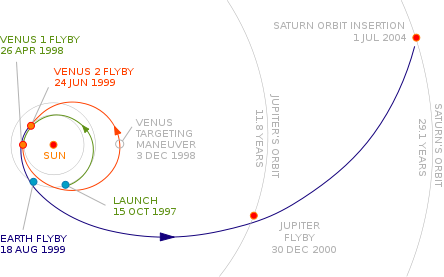
Le cas de la sonde Cassini-Huygens

La sonde Cassini-Huygens (sonde spatiale) a utilisé à plusieurs reprises l'assistance gravitationnelle pour parvenir à Saturne. Elle modifier son vecteur vitesse d'abord en passant à deux reprises près de Vénus puis la Terre et enfin Jupiter. L'utilisation de l'assistance gravitationnelle a allongé sa trajectoire qui a duré 6,7 ans au lieu des 6 ans nécessaires pour une orbite de transfert de Hohman mais elle a permis d'économiser un delta-V de 2 km/s permettant à cette sonde particulièrement lourde d'atteindre Saturne. Il aurait fallu donner une vitesse de 15,6 km/s à la sonde (en négligeant la gravité de Saturne et de la Terre ainsi que les effets de la trainée atmosphérique) pour la placer sur une trajectoire directe ce qu'aucun lanceur à l'époque n'aurait été capable de faire.

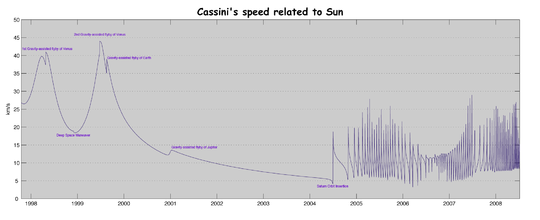Vitesse de Cassini par rapport au Soleil. L'effet de l'assistance gravitationnelle se traduit par les pics visibles sur la gauche du graphiques. Les pics de droite sont dus à l'orbite de la sonde autour de Saturne. La vitesse est indiquée en km/s. On peut remarquer que la vitesse minimale de la sonde autour de Saturne est égale à la vitesse orbitale de Saturne soir à peu près 5 km/s, vitesse qui a été atteinte par la sonde lorsqu'elle a été capturée par Saturne.

Référence

• Arrêté du 20 février 1995 relatif à la terminologie des sciences et techniques spatiales.

Voir aussi

• Liste des articles relatifs à l'astronautique

Liens externes

• Transferts d'orbite et assistance gravitationnelle
• Simulation paramétrable de l'assistance gravitationnelle (animation Flash)

• Portail de l’astronautique
• Portail de l’astronomie