- Approximation d'Euler
-
Méthode d'Euler
En mathématiques, la méthode d'Euler, nommée ainsi en l'honneur du mathématicien Leonhard Euler, est une procédure numérique pour résoudre par approximation des équations différentielles du premier ordre avec une condition initiale. C'est la plus simple des méthodes de résolution numérique des équations différentielles.
Sommaire
Équation différentielle
La méthode d'Euler est une méthode numérique élémentaire de résolution d'équations différentielles du premier ordre, de la forme
où
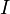 est un intervalle de
est un intervalle de  et
et 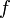 une fonction réelle sur
une fonction réelle sur 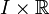 .
.Étant donnée une condition initiale
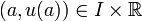 , la méthode fournit pour tout point
, la méthode fournit pour tout point 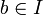 une suite
une suite 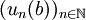 d'approximations de la valeur
d'approximations de la valeur 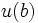 que prend, lorsqu'elle existe, la solution de l'équation qui correspond à cette condition initiale. Divers jeux de conditions sur
que prend, lorsqu'elle existe, la solution de l'équation qui correspond à cette condition initiale. Divers jeux de conditions sur 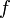 peuvent assurer la convergence de cette suite.
peuvent assurer la convergence de cette suite.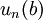 s'obtient en calculant
s'obtient en calculant 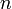 valeurs intermédiaires
valeurs intermédiaires ![(y_i)_{i\in[0,n]}](/pictures/frwiki/49/12296348875f2d7210b2ba69494f3b4e.png) de la solution approchée aux points
de la solution approchée aux points ![(x_i)_{i\in[0,n]}](/pictures/frwiki/52/4026e3d19e7561b834a777b88a6af801.png) régulièrement répartis entre
régulièrement répartis entre 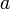 et
et 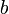 , donnés par
, donnés parEn étendant cette notation à
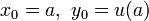 et
et 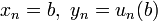 et en utilisant l'approximation de la dérivée
et en utilisant l'approximation de la dérivéeOn en déduit la relation suivante :
Les valeurs intermédiaires sont alors données par la relation de récurrence
qui est le schéma d'Euler explicite.
En remarquant, que l'on peut aussi approcher la dérivée en xi + 1 par la même relation
on en déduit la relation de récurrence
qui est le schéma d'Euler implicite. On notera que dans ce schéma, le terme yi + 1 apparaît des deux côtés de l'équation, ce qui contraint à utiliser des méthodes de résolution numérique du type de la relation de Newton-Raphson pour déterminer yi + 1 à chaque itération si la fonction
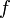 est non-linéaire.
est non-linéaire.Intégration d'une fonction
L'intégration d'une fonction continue sur un segment peut être vue comme un cas particulier où la fonction
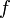 est continue et ne dépend que de
est continue et ne dépend que de 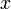 . On démontre alors aisément, en utilisant la continuité uniforme de
. On démontre alors aisément, en utilisant la continuité uniforme de 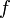 sur
sur ![[a,b]\](/pictures/frwiki/99/cfcbcc2c2a41716ab844e25069e87453.png) (théorème de Heine), que la suite
(théorème de Heine), que la suite 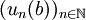 est de Cauchy, et donc converge par complétude de
est de Cauchy, et donc converge par complétude de  .
.Méthode d'Euler pour une fonction
Pour calculer des valeurs approchées d'une primitive G de f sur I = [x0, xn], on divise I en n intervalles et on choisit
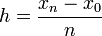
Pour la valeur initiale y0 on a F(x0) = G(x0) = y0 ce qui permet de placer le premier point A0 (x0 ; y0).
Pour les n valeurs x1 = x0 + h, x2 = x1 + h, …, xn = xn-1 + h, on calcule de proche en proche, en relation avec la propriété de la dérivée citée ci-dessus, les n valeurs approchées F(x1), F(x2)…, F(xn) de G.
En effet G est dérivable en x0 et G'(x0) = f(x0) :
F(x0 + h) = F(x0) + h f(x0) donc F(x1) = y0 + hG'(x0)
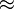 G(x1) ; soit y1 = y0 + h f(x0) et F(x1) = y1
G(x1) ; soit y1 = y0 + h f(x0) et F(x1) = y1 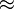 G(x1).
G(x1).On recommence avec x1 :
F(x1 + h) = F(x1) + h f(x1) donc F(x2) = y1 + hG'(x1)
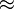 G(x1) + hG'(x1)
G(x1) + hG'(x1) 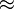 G(x2) ; soit y2 = y1 + h f(x1) et F(x2) = y2
G(x2) ; soit y2 = y1 + h f(x1) et F(x2) = y2 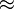 G(x2).
G(x2).Puis y3 = y2+ h f(x2) = F(x3)
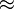 G(x3).
G(x3).Et ainsi de suite n itérations jusqu'à yn = yn-1 + h f(xn-1) = F(xn)
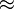 G(xn).
G(xn).Exemple :
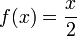
Étant donné la fonction
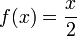 et des valeurs initiales x0 = 1 et
et des valeurs initiales x0 = 1 et 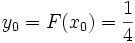 .
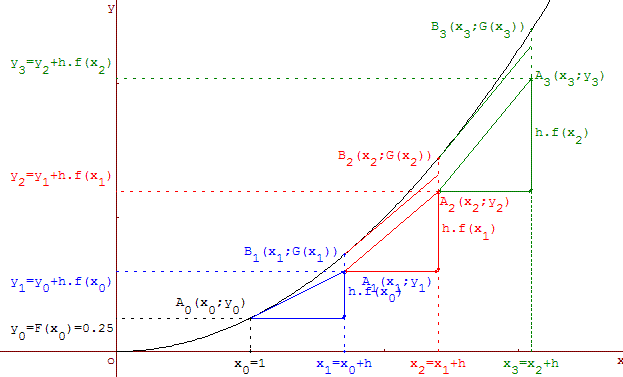
.Le calcul des valeurs F(x1), F(x2), F(x3)… permet d'obtenir la représentation graphique de F par les segments [A0A1], [A1A2], [A2A3]…
La fonction
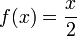 a pour primitive
a pour primitive 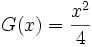 avec x0 = 1 et
avec x0 = 1 et 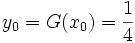 .
.La courbe (C) représentative de G est ici placée sur le même graphe pour visualiser le calcul des tangentes.
La fonction affine est une approximation de la primitive G.
Lien externe
Augmenter n pour diminuer h et obtenir de bien meilleurs résultats :
voir Méthode d'Euler - MIAM
- Portail des mathématiques
Catégorie : Équations différentielles numériques
Wikimedia Foundation. 2010.

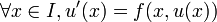
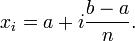
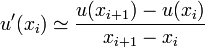
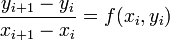
![y_{i+1} = y_i + (x_{i+1}-x_i)f(x_i, y_i),\ i\in[0,n-1].](/pictures/frwiki/55/7ed0d45679ae5ece32740249491f550f.png)
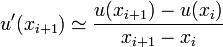
![y_{i+1} = y_i + (x_{i+1}-x_i)f(x_{i+1}, y_{i+1}),\ i\in[0,n-1].](/pictures/frwiki/55/7e8b892f8d6c0294ad6022fd32e4c0d6.png)