- Application numerique
-
Application numérique
En sciences, particulièrement en physique, l'application numérique est l'obtention de la valeur numérique d'une grandeur physique à partir de celles d'autre grandeurs lorsque l'on connaît une formule analytique reliant ces grandeurs.
En d'autres termes, il s'agit d'obtenir z = f(x,y) à partir des valeurs numériques de x et y, et de la fonction f. En physique, une difficulté s'ajoute : x et y ont des unités, et il faut s'assurer qu'elles sont compatibles.
Étapes d'une application numérique
Une application numérique se fait en plusieurs étapes :
- la conversion des données numériques dans des unités compatibles, par exemple dans le Système international ;
- le calcul numérique lui-même, souvent décomposé en plusieurs étapes pour diminuer le risque d'erreur et permettre de retrouver une erreur le cas échéant ;
- la conservation des chiffres significatifs pertinents, souvent seuls les deux ou trois premiers chiffres suffisent et sont porteur d'un véritable sens physique.
Exemple
La distance parcourue par un objet en chute libre h est relié au temps de chute t et à l'accélération de la pesanteur g par la formule :
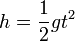 .
.
On considère un objet chutant pendant 500 millisecondes, sachant que sur terre g = 981 cm˙s-2.
- On convertit le temps de chute et l'accélération de la pesanteur dans le système international : t = 0,5 s et g = 9,81 m˙s-2.
- L'application numérique donne
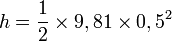 m
m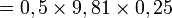 m
m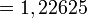 m
m
- Mais quelle précision doit-on donner à ce résultat ? Il est nécessaire de compter les chiffres significatifs des données présentes dans le problème : 0,5 soit un chiffre et 9,81 soit trois chiffres, le résultat ne doit comporter qu'un seul chiffre car 0,5 limite la précision : une hauteur de chute de 1 mètre.
- Faire une application numérique, c'est aussi connaître la précision du résultat que l'on prétend obtenir.
- Portail de la physique
Catégorie : Physique
Wikimedia Foundation. 2010.
