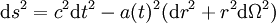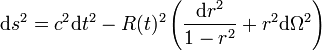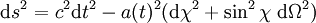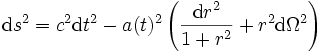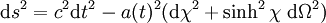Métrique de Friedman-Lemaître-Robertson-Walker

Métrique de Friedman-Lemaître-Robertson-Walker

Métrique de Friedmann-Lemaître-Robertson-Walker

En cosmologie, la métrique Robertson-Walker, souvent couplée aux équations de Friedmann-Lemaître du paramètre d'expansion R(t) (généralement abrégé modèle FLRW), est une métrique permettant de décrire un univers localement homogène et localement isotrope, en expansion ou contraction. Ce modèle est utilisé comme une première approximation du modèle cosmologique standard de l'univers, le Big Bang.

Selon les préférences géographiques ou historiques, le modèle FLRW est parfois désigné selon les noms d'une partie des quatre scientifiques Alexander Friedmann, Georges Lemaître, Howard Percy Robertson et Arthur Geoffrey Walker ; par exemple : Friedmann-Robertson-Walker (FRW) ou Robertson-Walker (RW).

Sommaire

Utilisation de la métrique FLRW pour décrire l'univers

Parce que le modèle FLRW suppose que l'univers est homogène, on pourrait en conclure que le modèle du Big Bang ne peut pas prendre en compte les fluctuations de densité présentes dans l'univers. En effet dans un modèle strictement FLRW, il n'y a aucun amas de galaxies, ni étoile, ni planète, ni êtres biologiques, puisque ces objets sont de loin plus denses que l'Univers en moyenne.

Il n'en est rien, car en réalité, le modèle FLRW est uniquement utilisé comme première approximation à cause de la simplicité qu'il apporte aux calculs; les modèles tenant compte des fluctuations de densité sont ensuite rajoutés au modèle FLRW. La plupart des cosmologistes s'accordent à ce que la partie de l'Univers observable est bien approximée par un modèle presque FLRW, c'est-à-dire un modèle qui suit la métrique FLRW à part des fluctuations primordiales de densité. En 2003, les implications théoriques de ces diverses extensions semblent bien comprises et le but est de les rendre cohérentes avec les observations effectuées par les satellites COBE et WMAP.

Pourtant, au risque d'oublier les différences entre le modèle parfaitement FLRW et le modèle perturbé, le modèle presque FLRW est normalement appelé simplement le modèle FLRW'

Formulation mathématique

En coordonnées polaires 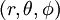(r, \theta, \phi) \;, elle peut être écrite comme :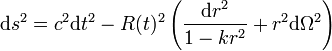

{\rm d}s^2 = c^2 {\rm d}t^2 - R(t)^2 \left (\frac{{\rm d}r^2}{1 - k r^2} + r^2 {\rm d}\Omega^2 \right )

ou bien, à l'aide d'un changement de coordonnées pour faire apparaître la distance comobile \chi \; :

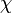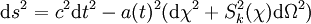
{\rm d}s^2 = c^2 {\rm d}t^2 - a(t)^2 ({\rm d}\chi^2 + S_k^2(\chi) {\rm d}\Omega^2 )

où

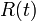  • R(t) \; est le rayon de courbure de l'univers et 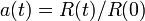a(t) = R(t)/R(0) \; est le facteur d'échelle de l'univers à l'époque t \;.
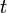  • Le paramètre 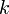k \; exprime la courbure spatiale et peut prendre trois valeurs : +1, 0 ou -1, caractérisant respectivement un espace courbe fermé (correspondant à une géométrie sphérique), un espace plat (correspondant à la géométrie euclidienne usuelle) et une espace courbe ouvert (correspondant à une géométrie hyperbolique)
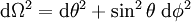  • \textstyle {\rm d}\Omega^2 = {\rm d}\theta^2 + \sin^2 \theta \; {\rm d} \phi^2 exprime les contributions de la métrique liées à la "direction" 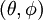(\theta, \phi) \;. Pour l'étude de l'expansion de l'univers, on prendra souvent 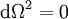{\rm d}\Omega^2 = 0 \;, puisqu'on considèrera les trajectoires radiales des photons suivant une géodésique.
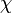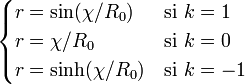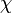  • \chi \; est défini tel que : \begin{cases} r = \sin (\chi/R_0) & \textrm{si\ } k = 1 \\ r = \chi/R_0 & \textrm{si\ } k = 0\\ r = \sinh (\chi/R_0) & \textrm{si\ } k = -1\\ \end{cases} où \chi \; permet de déterminer la distance comobile.
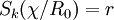  • S_k(\chi/R_0) = r \; (et peut être exprimée en fonction de χ directement à partir de la définition ci-dessus).

Métrique FLRW en fonction des valeurs de la courbure

Métrique FLRW dans un espace plat

Dans le cas où 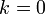k = 0 \;, on peut ré-écrire la métrique :

{\rm d}s^2 = c^2 {\rm d}t^2 - a(t)^2 ( {\rm d}r^2 + r^2 {\rm d} \Omega^2 ) \;

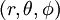
On retrouve ici la valeur classique de la métrique d'un espace usuel doté d'un facteur d'échelle, exprimé en coordonnées radiales (r, \theta, \phi) \;

Métrique FLRW dans un espace de courbure positive

Si 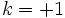k = +1 \;, on a

{\rm d}s^2 = c^2 {\rm d}t^2 - R(t)^2 \left (\frac{{\rm d}r^2}{1 - r^2} + r^2 {\rm d} \Omega^2 \right )

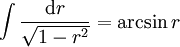On voit qu'en r = 1 on a une singularité : on va donc chercher un changement de coordonnées sur l'intervalle ]-1;1[ \; permettant de faire apparaître facilement la distance comobile. En remarquant que \int \frac{{\rm d}r}{\sqrt{1 - r^2}} = \arcsin r, on choisit 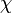\chi \; tel que 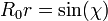R_0 r = \sin(\chi) \;. On obtient alors la nouvelle forme de la métrique :

{\rm d}s^2 = c^2 {\rm d}t^2 - a(t)^2 ( {\rm d} \chi^2 + \sin^2 \chi \; {\rm d} \Omega^2 ) \;

Métrique FLRW dans un espace de courbure négative

Si 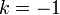k = -1 \;, on a

{\rm d}s^2 = c^2 {\rm d}t^2 - a(t)^2 \left (\frac{{\rm d}r^2}{1 + r^2} + r^2 {\rm d} \Omega^2 \right )

En remarquant que 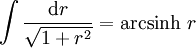\int \frac{{\rm d}r}{\sqrt{1 + r^2}} = \operatorname{arcsinh}\ r, on choisit comme changement de coordonnées 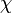\chi \; tel que 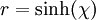r = \sinh(\chi) \;. On obtient alors la nouvelle forme de la métrique :

{\rm d}s^2 = c^2 {\rm d}t^2 - a(t)^2 ( {\rm d} \chi^2 + \sinh^2 \chi \; {\rm d} \Omega^2 ) \;

Voir aussi

Articles connexes


Quelques modèles cosmologiques
Atome primitif • Big Bang • Big Crunch • Big Rip • Classification de Bianchi • Cosmologie branaire • Cosmologie cordiste • Dimensions supplémentaires • Espace anti de Sitter • Espace de Sitter • Espace de Taub-NUT • Inflation cosmique • Modèle ΛCDM • Modèle cyclique • Modèle OCDM • Modèle SCDM • Modèle standard de la cosmologie • Pré Big Bang • Théorie de l'état stationnaire • Univers d'Einstein • Univers de Friedmann-Lemaître-Robertson-Walker • Univers de Gödel • Univers de Milne • Univers de de Sitter • Univers ekpyrotique • Univers en tore bidimensionnel • Univers fractal • Univers hésitant • Univers mixmaster • Univers phénix
  • Portail de la cosmologie Portail de la cosmologie
Ce document provient de « M%C3%A9trique de Friedmann-Lema%C3%AEtre-Robertson-Walker ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Métrique de Friedman-Lemaître-Robertson-Walker de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Friedman-Lemaître-Robertson-Walker — Métrique de Friedmann Lemaître Robertson Walker En cosmologie, la métrique Robertson Walker, souvent couplée aux équations de Friedmann Lemaître du paramètre d expansion R(t) (généralement abrégé modèle FLRW), est une métrique permettant de… …   Wikipédia en Français

  • Équation de Friedman — Équations de Friedmann Le contenu de cet article du Portail:Cosmologie a fait l objet d une validation par un chercheur spécialiste du domaine le 18 juillet 2007 (comparer avec la version actuelle). Il est donc en principe exempt d erreur grave.… …   Wikipédia en Français

  • Alexandre Friedmann — Pour les articles homonymes, voir Friedmann. Alexandre Friedmann Alexandre Friedmann Naissance 29  …   Wikipédia en Français

  • Jürgen Ehlers — (29 décembre 1929 – 20 mai 2008) était un physicien allemand, auteur de contributions notoires pour la compréhension de la théorie de la relativité générale d Albert Einstein. Après ces études de premier second cycle dans l équipe de relativité… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”