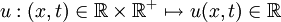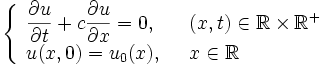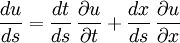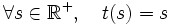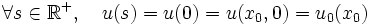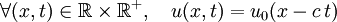Méthode Des Caractéristiques

Méthode des caractéristiques

En mathématiques, la méthode des caractéristiques est une technique permettant de résoudre les équations aux dérivées partielles. Particulièrement adaptée aux problèmes de transport, elle est utilisée dans de nombreux domaines tels que la mécanique des fluides ou le transport de particules.

Dans certains cas particuliers, la méthode des caractéristiques peut permettre la résolution purement analytique de l'EDP. Dans les cas plus complexes (rencontrés par exemple en modélisation des systèmes physiques), la méthode des caractéristiques peut être utilisée comme une méthode de résolution numérique du problème.

Sommaire

1 Méthode analytique
- 1.1 Principe général
- 1.2 Exemple : Résolution analytique de l'équation de transport
2 Méthode numérique
- 2.1 Principe général
- 2.2 Exemple

Méthode analytique

Principe général

Pour une équation aux dérivées partielles (EDP) du premier ordre, la méthode des caractéristiques cherche des courbes (appelées « lignes caractéristiques », ou plus simplement « caractéristiques ») le long desquelles l'EDP se réduit à une simple équation différentielle ordinaire (EDO). La résolution de l'EDO le long d'une caractéristique permet de retrouver la solution du problème original.

Exemple : Résolution analytique de l'équation de transport

On cherche une fonction $u$ :

$u: (x,t)\in\mathbb{R}\times\mathbb{R}^+ \mapsto u(x,t)\in\mathbb{R}$

solution du problème suivant:

$\left\{\begin{array}{l l} \displaystyle\frac{\partial u}{\partial t} + c\frac{\partial u}{\partial x} = 0, \quad & (x,t)\in\mathbb{R}\times\mathbb{R}^+\\ u(x,0) = u_0(x), & x\in\mathbb{R} \end{array}\right.$

dans laquelle $\textstyle c$ est une constante.

On cherche une ligne caractéristique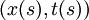 $\textstyle\left(x(s), t(s)\right)$ le long de laquelle cette EDP du premier ordre se réduirait à une EDO. Calculons la dérivée de $u$ le long d'une telle courbe :

$\frac{du}{ds} = \frac{dt}{ds}\,\frac{\partial u}{\partial t} + \frac{dx}{ds}\,\frac{\partial u}{\partial x}$

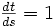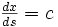On remarquera aisément qu'en imposant $\textstyle\frac{dt}{ds} = 1$ et $\textstyle\frac{dx}{ds} = c$ , on obtient : 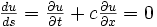$\textstyle\frac{du}{ds} = \frac{\partial u}{\partial t} + c\frac{\partial u}{\partial x} = 0$ . La solution de l'équation reste donc constante le long de la ligne caractéristique.

Nous nous retrouvons donc avec trois équations différentielles ordinaires à résoudre :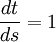

$\frac{dt}{ds} = 1$ : en posant 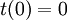$\textstyle t(0)=0$ , on obtient :

$\forall s\in\mathbb{R}^+, \quad t(s)=s$

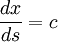$\frac{dx}{ds} = c$ : en notant 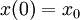$\textstyle x(0)=x_0$ , on obtient :

$\forall s\in\mathbb{R}^+, \quad x(s)=x_0+c\,s=x_0+c\,t$

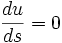$\frac{du}{ds} = 0$ :

$\forall s\in\mathbb{R}^+, \quad u(s) = u(0) = u(x_0,0) = u_0(x_0)$

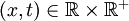Dans ce cas, les lignes caractéristiques sont donc des droites de pente $\textstyle c$ , le long desquelles la solution reste constante. La valeur de la solution en un point $\textstyle (x,t)\in\mathbb{R}\times\mathbb{R}^+$ peut donc être retrouvée en cherchant la valeur de la condition initiale 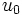$\textstyle u_0$ à l'origine 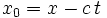$\textstyle x_0=x-c\,t$ de la ligne caractéristique:

$\forall (x,t)\in\mathbb{R}\times\mathbb{R}^+,\quad u(x,t) = u_0(x-c\,t)$

Méthode numérique

Principe général

Exemple

Portail des mathématiques

Ce document provient de « M%C3%A9thode des caract%C3%A9ristiques ».

Catégorie : Équation aux dérivées partielles

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Méthode Des Caractéristiques de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Methode des caracteristiques — Méthode des caractéristiques En mathématiques, la méthode des caractéristiques est une technique permettant de résoudre les équations aux dérivées partielles. Particulièrement adaptée aux problèmes de transport, elle est utilisée dans de nombreux … Wikipédia en Français
Méthode des caractéristiques — En mathématiques, la méthode des caractéristiques est une technique permettant de résoudre les équations aux dérivées partielles. Particulièrement adaptée aux problèmes de transport, elle est utilisée dans de nombreux domaines tels que la… … Wikipédia en Français
méthode des caractéristiques — charakteristikų metodas statusas T sritis fizika atitikmenys: angl. method of characteristics vok. Charakteristikenverfahren, n rus. метод характеристик, m pranc. méthode des caractéristiques, f … Fizikos terminų žodynas
Méthode des coûts complets — La méthode des coûts complets, déjà utilisée au XVIe siècle, consiste à calculer les coûts de production des produits (biens ou services) en répartissant les charges directes et indirectes de l entreprise (celles qui peuvent être affectées… … Wikipédia en Français
Methode des elements finis — Méthode des éléments finis Pour les articles homonymes, voir Élément. Solution bidimensionnelle d une équation magnétostatique obtenue par éléments fin … Wikipédia en Français
Méthode Des Éléments Finis — Pour les articles homonymes, voir Élément. Solution bidimensionnelle d une équation magnétostatique obtenue par éléments fin … Wikipédia en Français
Methode des volumes finis — Méthode des volumes finis En analyse numérique, la méthode des volumes finis est utilisée pour résoudre numériquement des équations aux dérivées partielles, comme la méthode des différences finies et la méthode des éléments finis. Mais,… … Wikipédia en Français
Méthode Des Volumes Finis — En analyse numérique, la méthode des volumes finis est utilisée pour résoudre numériquement des équations aux dérivées partielles, comme la méthode des différences finies et la méthode des éléments finis. Mais, contrairement à la méthode de… … Wikipédia en Français
Methode des temperatures — Méthode des températures La méthode des températures, aussi appelée méthode de la courbe thermique ou méthode Ogino Knaus ou encore méthode symptothermique est une méthode de contraception naturelle, ou, au contraire de conception naturelle.… … Wikipédia en Français
Méthode Des Températures — La méthode des températures, aussi appelée méthode de la courbe thermique ou méthode Ogino Knaus ou encore méthode symptothermique est une méthode de contraception naturelle, ou, au contraire de conception naturelle. Procédure Cette méthode est… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Méthode Des Caractéristiques