- Méthode Condorcet Avec Rangement Des Paires Par Ordre Décroissant
-
Méthode Condorcet avec rangement des paires par ordre décroissant
La méthode Condorcet avec rangement des paires par ordre décroissant est un système de vote qui permet de résoudre certains conflits de la méthode Condorcet. La méthode initialement proposée par Condorcet est développée par Tideman[1].
Sommaire
Principe
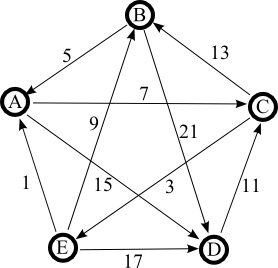
Chaque électeur range les candidats par ordre de préférence. Comme dans toute méthode Condorcet, toutes les confrontations par paires sont organisées. On établit alors un graphe orienté pondéré :
- les sommets sont les candidats ;
- entre chaque paire de candidats (X, Y) on crée un arc orienté de X vers Y auquel on donne la valeur n - p (n : nombre de victoires de X sur Y, p : nombre de défaites).
- on classe chaque arc par poids décroissant, selon un ordre strict (sans ex-aequo) ; pour cela, si nécessaire, refaire la pondération (par exemple : à n - p égal, donner un poids un peu supérieur à l'arc pour lequel p est plus faible ; d'autre variantes sont possibles et celle-ci n'est pas toujours suffisante).
Puis on parcourt le graphe, par ordre décroissant du poids attribué, en recherchant systématiquement les cycles, et en "confirmant" les arcs qui n'en créent pas (à l'inverse, on élimine les arcs qui créent un cycle avec les arcs déjà confirmés). Au terme des opérations on obtient un graphe sans cycles. Le gagnant est le sommet vers lequel n'arrive aucune flèche (c'est-à-dire : qui gagne tous les duels "confirmés").
Pour cela, il aura fallu parcourir, au maximum et pour N candidats, N(N-1)/2 arcs.
Exemple
45 votants; 5 candidats:
- 5 ACBED
- 5 ADECB
- 8 BEDAC
- 3 CABED
- 7 CAEBD
- 2 CBADE
- 7 DCEBA
- 8 EBADC
On effectue les confrontations par paires (méthode Condorcet)
d[*,A] d[*,B] d[*,C] d[*,D] d[*,E] d[A,*] 20 26 30 22 d[B,*] 25 16 33 18 d[C,*] 19 29 17 24 d[D,*] 15 12 28 14 d[E,*] 23 27 21 31 Matrice des duels entre candidats On donne leur poids et leur orientations aux arcs (A bat B 20 fois, alors que B bat A 25 fois : cela donne un arc orienté de B vers A et de poids 25-20=5)
d[*,A] d[*,B] d[*,C] d[*,D] d[*,E] d[A,*] 7 15 d[B,*] 5 21 d[C,*] 13 3 d[D,*] 11 d[E,*] 1 9 17 Matrice des arcs entre candidats On constitue le graphe orienté des duels en classant les 10 arcs restants par ordre d'examen, du premier ( BD, dont le poids est 21) au dernier ( EA, dont le poids est 1) : (BD), (ED), (AD), (CB), (DC), (EB), (AC), (BA), (CE), (AE)
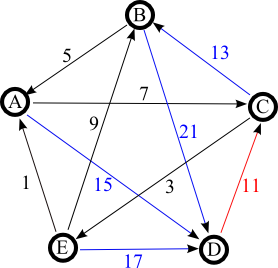
Les arcs (BD), (ED), (AD) , (CB) sont confirmés car ils ne construisent pas de cycle, mais l'arc (DC) doit être supprimé car il créerait le cycle (BDCB)
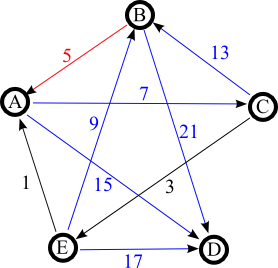
Puis les arcs (EB) et (AC) sont confirmés (en bleu) mais l'arc (BA) doit être supprimé (mis en rouge) car il créerait le cycle (ACBA)
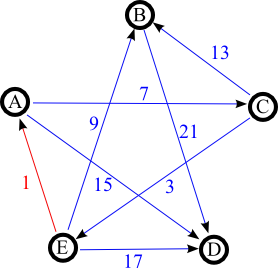
Enfin l'arc (CE) est conservé et l'arc (AE) est supprimé.
Le graphe orienté donne alors pour gagnant le candidat A, La méthode Schulze et la méthode Black aurait donné le candidat E.
Critères respectés
Article détaillé : Critères de systèmes de vote.- Cette méthode respecte : les critères du gagnant de Condorcet, du perdant de Condorcet, des clones, d'indépendance locale, de la majorité, de la monotonie, de majorité mutuelle, de Paréto, de symétrie par inversion et de Smith.
- Elle ne respecte pas : les critères de consistance et de préférence secrète.
Voir aussi
Notes
- ↑ Nicolaus Tideman (1943 - ), professeur d'économie , USA
Lien interne
Catégorie : Système électoral
Wikimedia Foundation. 2010.