Modèle des urnes d'ehrenfest

Le modèle des urnes est un modèle stochastique introduit en 1907 par les époux Ehrenfest pour illustrer certains des « paradoxes » apparus dans les fondements de la mécanique statistique naissante^[1]. Peu de temps en effet après que Boltzmann eut publié son théorème H, des critiques virulentes furent formulées, notamment par Loschmidt, puis par Zermelo, Boltzmann étant accusé de pratiquer des « mathématiques douteuses ».

Ce modèle est parfois également appelé le « modèle des chiens et des puces^[2] ». Le mathématicien Mark Kac a écrit à son propos qu'il était :

« ... probablement l'un des modèles les plus instructifs de toute la physique ... »

Le modèle des urnes

Définition du modèle stochastique

On considère deux urnes A et B, ainsi que N boules, numérotées de 1 à N. Initialement, toutes les boules se trouvent dans l'urne A. Le processus stochastique associé est construit de la façon suivante :

• A l'instant t₀ = 0, on tire au hasard un numéro i compris entre 1 et N, et on transfère la boule n°i de l'urne A vers l'urne B.

• A l'instant t₁ = 1, on tire à nouveau au hasard un numéro j compris entre 1 et N.
  • Si la boule n°j est dans l'urne A, on la transfère dans l'urne B.
  • Si la boule n°j est dans l'urne B, on la transfère dans l'urne A.

• Et ainsi de suite ...

Dynamique du modèle

N = 500 boules ; 10000 tirages.

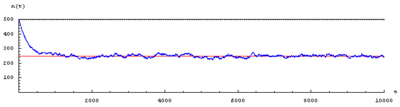
Dans ce modèle, on suit au cours du temps t (discret) le nombre total de boule n(t) présentes dans l'urne A. On obtient une courbe qui part initialement de n(0)=N et commence par décroître vers la valeur moyenne N/2, comme on pourrait s'y attendre pour un « bon » système thermodynamique initialement hors d'équilibre et relaxant spontanément vers l'équilibre.

N = 4 boules ; 100 tirages. Les fluctuations autour de la moyenne sont importantes lorsque N est petit, et les récurrences à l'état initial sont particulièrement visibles.

Mais cette décroissance est irrégulière : il existe des fluctuations autour de la valeur moyenne N/2, qui peuvent devenir parfois très importantes (ceci est particulièrement visible lorsque N est petit).

En particulier, quel que soit le nombre de boules N fini, il existe toujours des récurrences à l'état initial, pour lesquelles toutes les boules reviennent dans l'urne A après une durée finie. Mais, comme le temps moyen entre deux récurrences consécutives croit très rapidement avec N, ces récurrences ne nous apparaissent pas lorsque N est très grand (typiquement en physique statistique, N est de l'ordre de grandeur du nombre d'Avogadro).

Version « modèle des chiens et des puces »

Dans cette version, les deux urnes sont remplacées par deux chiens, et les N boules par N puces, sautant d'un chien à l'autre.

Récurrences & théorème de Kac (1947)

Récurrences à l'état initial

Il existe des récurrences à l'état initial, caractérisées par une suite dénombrable d'instants 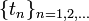finis pour lesquels toutes les boules reviennent dans l'urne A, c’est-à-dire que l'on a : n(t_n) = N (par convention, on pose t₀ = 0). On peut alors définir une nouvelle suite dénombrable τ_n = t_n − t_{n − 1} des durées finies entre deux récurrences consécutives.

Théorème de Kac (1947)

Il est possible de calculer la durée moyenne entre deux récurrences à l'état initial consécutives :

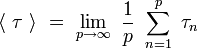
On a le théorème suivant [Kac - 1947] :

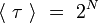
De plus, on peut montrer que la dispersion des durées autour de leur valeur moyenne, caractérisée par l'écart-type σ, est du même ordre de grandeur :

Voir par exemple [Kac-1957].

Exemples de simulations numériques

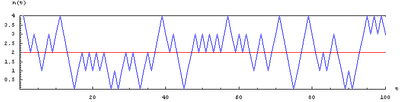
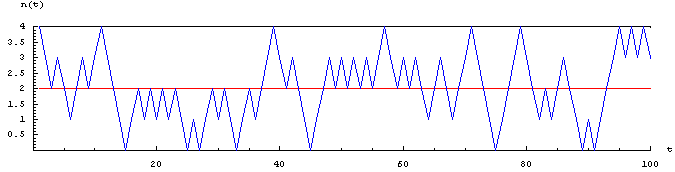N = 4 boules ; 100 tirages. Les récurrences à l'état initial sont très fréquentes.

Les grandes fluctuations relatives autour de la moyenne deviennent de moins en moins fréquentes pour une durée donnée lorsque le nombre N de boules augmente.

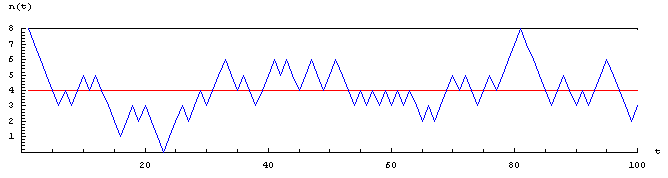N = 8 boules ; 100 tirages. Les récurrences à l'état initial semblent moins fréquentes sur la même durée.

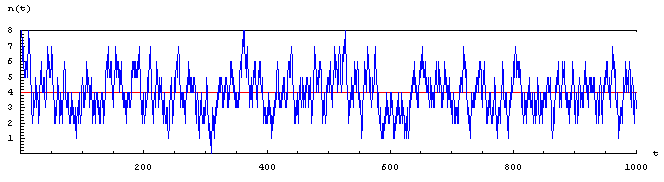N = 8 boules ; 1000 tirages. Les récurrences à l'état initial restent en fait fréquentes sur une plus longue durée.

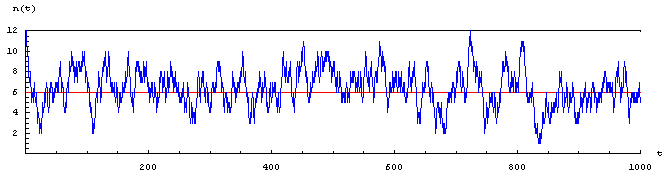N = 12 boules ; 1000 tirages.

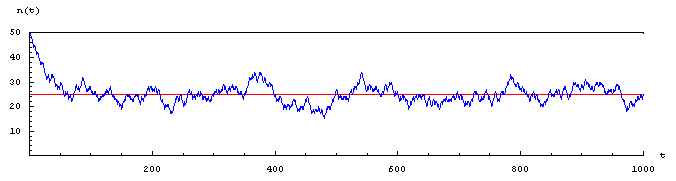N = 50 boules ; 1000 tirages.

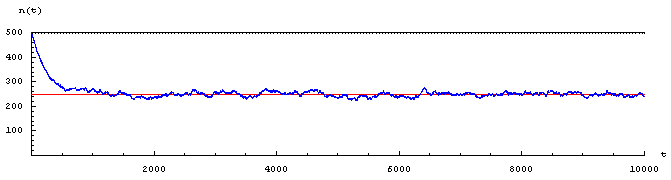N = 500 boules ; 1000 tirages.

Solution exacte

Voir par exemple : [Kac-1947] et : [Kac-1957]

Lien avec une marche aléatoire

Le modèle des urnes d'Ehrenfest est formellement similaire à une marche aléatoire non isotrope sur le réseau , dont la limite continue converge vers le mouvement brownien d'une particule élastiquement liée. En termes probabilistes on parle de convergence vers le processus d'Ornstein-Uhlenbeck.

Voir par exemple : [Kac-1947] et : [Kac-1957]

Articles connexes

• Physique statistique
• Théorème H
• Théorème de récurrence
• Hypothèse ergodique
• Théorie ergodique
• Chaîne de Markov
• Processus stochastique
• Marche aléatoire
• Mouvement brownien

Bibliographie

• Paul Ehrenfest & Tatiana Ehrenfest ; Ueber zwei bekannte Eingewände gegen das Boltzmannsche H-Theorem, Zeitschrift für Physik 8 (1907), 311-314.

• Mark Kac ; Random Walk and the Theory of Brownian Motion, American Mathematical Monthly 54(7) (1947), 369-391. Texte au format pdf. Cet article est l'un des six contenus dans : Selected Papers on Noise & Stochastic Processes, Charles Proteus Steinmetz & Nelson Wax (eds.), Dover Publishing, Inc. (1954). Réédité dans la collection Phoenix (2003), ASIN 0486495353.

• Mark Kac ; Probability and Related Topics in Physical Science, Lectures in Applied Mathematics Series 1a, American Mathematical Society (1957), ISBN 0821800477.

• Gérard Emch & Chuang Liu ; The logic of thermo-statistical physics, Springer-Verlag (2002), ISBN 3-540-41379-0.

• Enrico Scalas, Edgar Martin & Guido Germano ; The Ehrenfest urn revisited: Playing the game on a realistic fluid model, Physical Review E 76 (2007), 011104. ArXiv: cond-mat/0512038

Notes

• Portail des probabilités et des statistiques
• Portail de la physique