Modèle de régression multiple postulés et non postulés

Sommaire 1 Modèle 2 Régression multiple 3 Modèle postulé 4 Le problème de la sélection des variables explicatives 5 Modèle non postulé 6 Décomposition harmonique 7 Exemples 7.1 Application au marketing 7.2 Amélioration de la qualité industrielle 8 Références

Modèle

Un modèle relie une ou plusieurs variables à expliquer Y à des variables explicatives X, par une relation fonctionnelle Y = F(X)

• Un modèle physique est un modèle explicatif soutenu par une théorie.
• Un modèle statistique, au contraire, est un modèle empirique issu de données disponibles, sans connaissance a priori sur les mécanismes en jeu. On peut cependant y intégrer des équations physiques (lors du pré traitement des données).

Régression multiple

C’est le plus utilisé des modèles statistiques.

On dispose de n observations (i = 1,…, n ) de p variables. L'équation de régression s'écrit

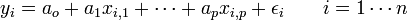
où

• ε_i est l'erreur du modèle;
• a₀, a₁, …, a_p sont les coefficients du modèle à estimer.

Le calcul des coefficients a_j et de l'erreur du modèle, à partir des observations, est un problème bien maîtrisé (voir la Régression linéaire multiple).

Plus délicat est le choix des variables entrant dans le modèle. Il peut être postulé ou non postulé.

Modèle postulé

Dans le modèle précédent, seuls les coefficients sont « dirigés par les données », la structure polynomiale du modèle est imposée par l’utilisateur (selon son expertise du problème), qui postule a priori :

• le type de modèle : linéaire ou polynomial, et le degré du polynôme,
• les variables qui entreront dans le modèle.

Exemple de modèle polynomial avec deux variables explicatives :

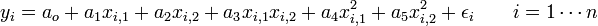
Le problème de la sélection des variables explicatives

Lorsque le nombre de variables explicatives est grand, il peut se faire que certaines variables soient corrélées entre elles. Dans ce cas il faut éliminer les doublons. Les logiciels utilisent pour ce faire des méthodes de sélection pas à pas (ascendante, descendante ou mixte).

Il n’en reste pas moins que la qualité du modèle final repose en grande partie sur le choix des variables, et le degré du polynôme.

Modèle non postulé

Le modèle « non postulé » est au contraire entièrement « dirigé par les données », aussi bien sa structure mathématique que ses coefficients.

La sélection des variables explicatives ne demande pas de connaissance a priori sur le modèle : elle a lieu parmi un ensemble très grand de variables, comprenant :

• les variables explicatives simples : A, B, C,... (proposées par les experts du domaine considéré et dont le nombre p peut être supérieur à n) ;
• des « interactions » ou « couplage » de ces variables, par exemple « A*B » (produit croisé sur variables centrées-réduites), mais aussi des « interactions logiques » tel « A et B », « A ou B », « A et B moyens », « A si B est fort », « A si B est moyen », « A si B est faible », etc. ;
• des fonctions de ces variables : par exemple cos(A) ou n’importe quelle fonction sinusoïdale amortie ou amplifiée, fonction périodique non sinusoïdale, effet de seuil, etc.

La sélection est faite avant le calcul des coefficients de la régression selon le principe suivant :

On cherche le facteur, ou l'« interaction », ou la fonction, le mieux corrélé à la réponse. L'ayant trouvé, on cherche le facteur, ou l'interaction, le mieux corrélé au résidu non expliqué par la corrélation précédente; etc. Cette méthode vise à ne pas compter deux fois la même influence, lorsque les facteurs sont corrélés, et à les ordonner par importance décroissante.

La liste trouvée, classée par ordre d’importance décroissante, ne peut pas compter plus de termes que d’inconnues (n). Si l’on ne garde qu’un terme dans le modèle, ce devra être le premier de la liste. Si l’on n’en garde que deux, ce seront les deux premiers, etc.

En effet, puisque chacun des termes de la liste "explique" le résidu non expliqué par les précédents, les derniers n'expliquent peut-être que du "bruit". Quel critère d'arrêt choisir ?

Le nombre de termes conservés dans le modèle peut être, par exemple, celui qui minimise l’erreur standard de prédiction SEP (Standard error of Prediction), ou celui qui maximise le F de Fisher. Ce nombre de terme peu aussi être choisi par l’utilisateur à partir de considérations physiques.

Exemple : on suppose que l’ensemble des « variables explicatives » candidates est {A,B,C,D,E,F,G}, et que le modèle obtenu est :

Y = constante + a.A + b.(« E et G ») + c.(« D et F moyens »)

On remarque que

* les variables B et C, non pertinentes, ne figurent pas dans le modèle

* la variable A est apparue comme terme simple,

* les variables E et G d’une part, et D et F, d’autre part, n’apparaissent que comme « interactions logiques ».

Ce modèle « parcimonieux »,c'est-à-dire comportant peu de termes (ici trois), fait intervenir 5 variables, et collera mieux à la réalité physique qu’un modèle polynomial. En effet la conjonction « E et G » qui signifie « E et G forts simultanément » est plus souvent rencontrée dans la réalité physique (exemple : la catalyse en chimie) qu'un terme polynomial de type E.G.

Décomposition harmonique

Un modèle non postulé sera également efficace dans la décomposition harmonique des séries.

En effet, le principe s'applique aussi bien en cas d’échantillonnage irrégulier (où les méthodes de type moyenne mobile, ARIMA ou Box et Jenkins sont mises en défaut) que dans les cas non stationnaires (où l’analyse de Fourier ne s’applique pas). Il permet de déceler et démêler les interférences de divers cycles et saisonnalités avec des ruptures de tendances en « marches d'escaliers », en « V » , des « ruptures logistiques », des motifs périodiques, et des événements accidentels tels que des pics isolés ou des « morceaux d'ondes ».

Exemples

Application au marketing

Les données de cet exemple sont disponibles sur internet (voir Effet Prix Promo Colas [1])

Dans un magasin de grande surface, deux produits sont présentés à la vente. Les gondoles peuvent être, ou non, mises en avant, les prix peuvent varier, de même que la fréquentation du magasin.

Voici les modèles non postulés obtenus pour chacun des deux produits :

1VENTES = 311.6 - 1386. Pri]1GondoleEnAvant + 492.4 Fréq&2Prix

R2a = 0.849, Q2 = 0.841, F = 220.4 , SEP= 86.28

2VENTES = 396.1 - 1701. (2Pri-2GondoleEnAvant) + 346.0 Fréq]1Prix

R2a = 0.854, Q2 = 0.851, F = 229.3, SEP= 81.27

Les termes de ces équations sont rangés par importance décroissante, et leur influence positive ou négative dépend du signe des coefficients.

D’où, compte tenu de la signification des symboles d’interactions logiques, l’on déduit que :

• Les ventes du produit 1 diminuent lorsque son prix augmente, si la gondole est mise en avant. Elles augmentent avec la fréquentation du magasin, si le prix du produit 2, concurrent ,est fort.
• Les ventes du produit 2 diminuent lorsque son prix augmente, augmentent lorsque la gondole est mise en avant. Elles augmentent aussi avec la fréquentation du magasin, si le prix du produit 1, concurrent, est fort.

Il est souvent utile d’associer aux modèles une analyse de données de type Iconographie des corrélations :

Marketing prix promo

Figure 1, analyse des liens.

Traits pleins : corrélations positives remarquables.

Pointillés : corrélations négatives remarquables.

D'une part, on remarque les liens positifs des ventes du produit 1 avec :

• la fréquentation,
• la mise en avant de la gondole de présentation.
• le prix du produit 2, concurrent.

D'autre part les liens négatifs des ventes du produit 1 avec :

• le prix du produit 1
• la mise en avant du produit 2, concurrent.

Amélioration de la qualité industrielle

Les données de Kackar (1985) utilisées ici ont servi d’illustration à diverses techniques de traitement de données. Voir D. Collombier : Plan d’expériences et amélioration de la qualité industrielle. Une alternative à la méthode Taguchi. RSA, tome 40, n°2 (1992), p.31-43. [2]

On veut améliorer le cintrage de ressorts à lame servant à la suspension de camions. Les lames sont chauffées dans un four, cintrées sous presse, puis refroidies dans un bain d’huile. On souhaite obtenir un flèche de cintrage proche de 8 pouces.

Les facteurs contrôlés de la fabrication, à deux niveaux (une valeur faible et une valeur forte), sont :

• T°Four = température du four (1840 et 1880°F)
• tChauffage = durée de chauffage (25 et 23 sec.)
• tTransfertFourPresse = durée du transfert four-presse (10 et 12 sec)
• tSousPresse = temps sous presse (2 et 3 sec.)

• T°Refroidissement = température de refroidissement. Difficile à contrôler en cours de fabrication, elle peut l’être seulement lors des essais. On la traite comme un facteur de bruit à deux niveaux (130-160°F et 150-170°F)

Le plan d’expériences choisi, comprenant 8 essais (pour les facteurs de fabrication), est donc répété deux fois, pour chacune des températures de refroidissement. Soit 16 essais.

En outre chacun des essais est répété 3 fois pour prendre en compte les sources de bruit non contrôlées. Soit au total 48 essais.

Les réponses de l’expérience sont

• Ymoy = flèche moyen pour la faible température de refroidissement (moyenne sur 3 mesures)
• Ymoy = flèche moyen pour la forte température de refroidissement (moyenne sur 3 mesures)
• Rapport Signal/Bruit = calculé d’après les 6 mesures par essai de fabrication.

Dans le tableau suivant, les niveaux des facteurs de fabrication sont noté -1 pour faible, et 1 pour fort. Le niveau de température de refroidissement est noté 1 pour faible et 2 pour fort.

	T°Four	tChauffage	tTransfert FourPresse	tSousPresse	T°Refroid	Ymoy	Signal/Bruit
1	-1	-1	-1	-1	1	7.79	5,426739
2	-1	-1	-1	-1	2	7.29	5,426739
3	1	-1	-1	1	1	8.07	11,6357
4	1	-1	-1	1	2	7.733	11,6357
5	-1	1	-1	1	1	7.52	6,360121
6	-1	1	-1	1	2	7.52	6,360121
7	1	1	-1	-1	1	7.63	8,658226
8	1	1	-1	-1	2	7.647	8,658226
9	-1	-1	1	1	1	7.94	7,337677
10	-1	-1	1	1	2	7.4	7,337677
11	1	-1	1	-1	1	7.947	10,44231
12	1	-1	1	-1	2	7.623	10,44231
13	-1	1	1	-1	1	7.54	3,700976
14	-1	1	1	-1	2	7.203	3,700976
15	1	1	1	1	1	7.687	8,860563
16	1	1	1	1	2	7.633	8,860563

Voici les modèles non postulés obtenus pour le flèche Ymoy et pour le rapport Signal/Bruit :

Ymoy = 7.636 - 0.5687 tCha^T°Refroid + 0.3174 (T°Fo+tSousPresse) - 0.3127 T°Re&-T°Four

R2a = 0.934, Q2 = 0.918, F = 71.59, SEP= 0.7446E-01

Signal/Bruit = 7.803 + 7.449 (T°Fo-tChauffage) + 4.201 T°Fo^tSousPresse + 1.874 tCha]-T°Four

R2a = 0.969, Q2 = 0.964, F = 155.3, SEP= 0.5413

Les termes de ces équations sont rangés par importance décroissante (chacun expliquant le résidu non expliqué par les précédents), et leur influence positive ou négative dépend du signe des coefficients.

D’où, compte tenu de la signification des symboles d’interactions logiques, l’on déduit que :

• La réponse moyenne diminue si tChauffage ou T°Refroidissement diminuent ; le résidu non expliqué par les termes précédents augmente si T°Four +tSousPresse augmente ; et enfin le résidu de ces résidus non expliqués diminue si T°refroidissement augmente en même temps que diminue T°Four.
• Le rapport Signal/Bruit augmente (donc la dispersion diminue) quand T°Four augmente, et aussi lorsque tChauffage diminue ; le résidu non expliqué par les termes précédents augmente avec T°Four ou tSousPresse ; et enfin le résidu de ces résidus non expliqués augmente avec tChauffage si T°Four est faible.

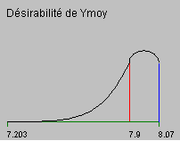
Ces modèles permettent (par de multiples tirages en faisant varier les facteurs), de trouver le compromis optimum pour un flèche moyen Y de 8 pouces avec un rapport Signal/bruit élevé. On peut pour cela définir des courbes de désirabilités (le désir global est un compromis des deux) :

Le tableau suivant donne dans la colonne "Choix", les valeurs favorisant ce compromis. Elles pourront faire l'objet d'un essai de validation.

	Bas	Haut	Choix
T°Four	-1	1	0.99
tChauffage	-1	1	-0.92
tTransfertFourPresse	-1	1	0
tSousPresse	-1	1	0.17
T°Refroid	1	2	1.03
Ymoy	7,203	8,07	7.98
Signal/Bruit	3,701	11,636	11.04

Pour une vision plus synthétique du phénomène on peut associer aux modèles une analyse de données de type Iconographie des corrélations :

Figure 2, analyse des liens.

Traits pleins : corrélations positives remarquables.

Pointillés : corrélations négatives remarquables.

D'une part, on remarque les liens positifs de Ymoy (flèche des ressorts) avec :

• le rapport Signal/Bruit,
• la T°Four.

D'autre part les liens négatifs Ymoy avec:

• la durée tChauffage
• la température de refroidissement.

Quant au rapport Signal/Bruit il dépend

• positivement de T°Four,
• négativement de tChauffage.

Références

[3] Lesty M. (1999) Une nouvelle approche dans le choix des régresseurs de la régression multiple en présence d’interactions et de colinéarités. La revue de Modulad, n°22, janvier 1999, pp. 41-77

[4] Lesty M. (2002) La recherche des harmoniques, une nouvelle fonction du logiciel CORICO. La revue de Modulad, n°29, juin 2002, pp. 39-77

• Portail des probabilités et des statistiques