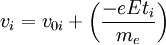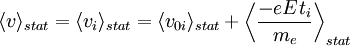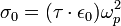- Modèle De Drude
-
Modèle de Drude
Le modèle de Drude (du nom du physicien Paul Drude) est une adaptation effectuée en 1900 de la théorie cinétique des gaz aux électrons des métaux (découverts 3 ans plus tôt, en 1897 par J.J. Thomson). En considérant les électrons d'un métal comme des particules classiques ponctuelles confinées à l'intérieur du volume défini par l'ensemble des atomes de l'échantillon, on obtient un gaz qui est entraîné dans un mouvement d'ensemble (lequel se superpose au mouvements individuels des particules) par des champs électriques et magnétiques et freiné dans ce mouvement par des collisions. Les collisions envisagées par Drude sont les collisions sur les cœurs d'atomes. Bien que se basant sur des hypothèses démenties depuis (description purement classique du mouvement des électrons), il permet de rendre compte de plusieurs propriétés des métaux comme la conductivité électrique, la conductivité thermique et l'effet Hall.
Le modèle repose sur les hypothèses suivantes :
- Le système est assimilé à un ensemble de n électrons de charge − e par unité de volume, placés dans un milieu de particules ponctuelles de masse m sans interaction entre elles.
- On peut décrire classiquement les électrons.
- Les électrons subissent des collisions. La probabilité de subir une collision entre t et t + dt est donnée par
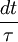 , où τ est le temps moyen entre deux collisions consécutives, appelé égalememt le temps de relaxation.
, où τ est le temps moyen entre deux collisions consécutives, appelé égalememt le temps de relaxation.
Les collision auxquelles sont soumis les électrons étaient aux yeux de Drude les collisions avec les noyaux atomiques du réseau cristallin. En réalité, il s'agit de ce que l'on appelle des collisions entre électrons et phonons.
La présence des collisions a pour conséquence une force de frottement visqueux de la forme
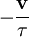 où
où 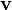 est la vitesse de l'électron.
est la vitesse de l'électron.On a alors, en appliquant la loi d'Ohm
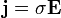 , l'expression de la conductivité :
, l'expression de la conductivité : 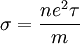 .
.Sommaire
Conductivité du courant continu
On considère que les électrons sont accélérés uniformément par le champ électrique E durant un intervalle de temps entre deux collisions. À la fin de ce laps de temps, à la suite de la collision, ils sont statistiquement relaxés dans leur état cinétique initial.
À tout instant, chaque ie électron a donc une vitesse vi qui s'écrit
où vi = v0i est la vitesse initiale de l'électron i à l'issue du dernier choc et ti le temps écoulé depuis celui-ci. La vitesse moyenne (au sens de la moyenne d'ensemble) qui décrit les électrons est :
Comme
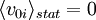 (hypothèse de chocs parfaitement aléatoires avec vitesses finales résultantes réparties autour d'une moyenne nulle) et
(hypothèse de chocs parfaitement aléatoires avec vitesses finales résultantes réparties autour d'une moyenne nulle) et 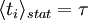 (hypothèse ergodique) on obtient la formule
(hypothèse ergodique) on obtient la formule 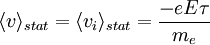 . On en déduit l'expression du courant électrique
. On en déduit l'expression du courant électriqueet celle de la conductivité
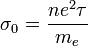 .
.
On peut faire apparaître la fréquence de plasma ωp en écrivant :
Conductivité en courant alternatif
Relations entre la constante diélectrique et la conductivité
Pour calculer la conductivité dans un champ électromagnétique, nous partons des équations de Maxwell, nommément
Loi Expression mathématique « Loi de Coulomb » 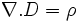
« Loi d'Ampère » 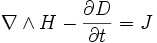
« Loi de Faraday » 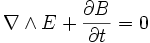
« Absence de monopôles magnétiques » 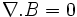
De ces équations nous tirons la relation entre la conductivité
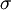 et la constante diélectrique
et la constante diélectrique 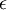 :
: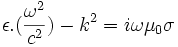
Calcul de la conductivité
Si nous décrivons le gaz d'électrons par sa matrice densité
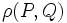 , celle-ci vérifie l'équation d'évolution :
, celle-ci vérifie l'équation d'évolution :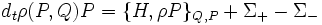
où
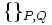 représente le crochet de Poisson et
représente le crochet de Poisson et 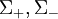 les termes de source et de destruction. Posons maintenant que l'hamiltonien
les termes de source et de destruction. Posons maintenant que l'hamiltonien 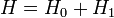 et que
et que 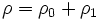 , où
, où 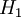 et
et 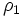 représentent des termes perturbatifs. L'équation initiale se réécrit alors sous la forme :
représentent des termes perturbatifs. L'équation initiale se réécrit alors sous la forme :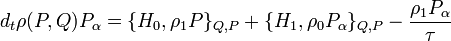
En remarquant l'indépendance de
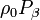 de
de 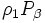 et de
et de 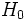 par rapport à
par rapport à 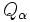 (homogénéité de la distribution des charges et invariance spatiale du hamiltonien non perturbé), il vient que la solution au premier ordre de la distribution perturbée s'écrit :
(homogénéité de la distribution des charges et invariance spatiale du hamiltonien non perturbé), il vient que la solution au premier ordre de la distribution perturbée s'écrit :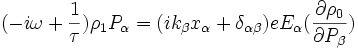
En posant l'approximation des grandes longueurs d'onde (et donc k petit) on trouve la forme de la conductivité:
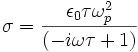
Conductivité thermique d'un métal
Il convient de doubler l'équation de transport du courant (c’est-à-dire de transport des particules) par une équation de transport de la chaleur :
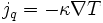
on obtient alors que le rapport
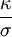 des conductivités thermique et électrique est directement proportionnel à la température, le coefficient de proportionnalité étant désigné par le nombre de Lorenz :
des conductivités thermique et électrique est directement proportionnel à la température, le coefficient de proportionnalité étant désigné par le nombre de Lorenz :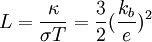
Cette loi de proportionnalité est connue sous le nom de loi de Wiedemann et Franz. Le résultat numérique indiqué ci-dessus vaut à peu près la moitié des valeurs obtenues expérimentalement. L'utilisation de la théorie du transport et du modèle quantique permet d'accéder à une valeur plus proche de la réalité pour le rapport
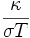 (c'est-à-dire le nombre de Lorenz), la valeur obtenue étant alors :
(c'est-à-dire le nombre de Lorenz), la valeur obtenue étant alors :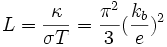
- Portail de la physique
Catégories : Électricité | Physique du solide
Wikimedia Foundation. 2010.