Module (nombres complexes)

Module d'un nombre complexe

Cet article vient en complément à nombre complexe.

Le module d'un nombre complexe z est un réel positif, noté |z|, qui mesure sa « taille » et généralise la valeur absolue d'un nombre réel. En coordonnées cartésiennes, z s'écrit a+ib où i est l'unité imaginaire, a est la partie réelle de z et b sa partie imaginaire. Le module de z est donné par

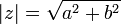$|z|=\sqrt{a^2+b^2}$ .

Le terme module a été introduit par Jean-Robert Argand dans son Essai sur une manière de représenter les quantités imaginaires par des constructions géométriques^{[réf. nécessaire]}.

Exemples

Le module de 0 est 0. Le module d'un nombre complexe non nul est non nul.
Le module d'un réel est sa valeur absolue.
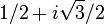Le module de 1+i est $\sqrt{2}$ . Comme expliqué dans cette vidéo, la racine carrée de $1/2+i\sqrt{3}/2$ a pour module 1.

Propriétés

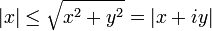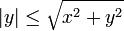Pour tous réels x et y, $|x|\leq \sqrt{x^2+y^2}=|x+iy|$ et $|y|\leq \sqrt{x^2+y^2}$ (|x| et |y| valeurs absolues respectives de x et y). Les propriétés suivantes sont vérifiées pour tout nombre complexe z, z₁ et z₂ :

${\left| z \right|} \ge 0\,$
${\left| z \right|} = 0 \Leftrightarrow z = 0\,$
${\left| z_1 . z_2 \right|} = \left| z_1 \right| . \left| z_2 \right|\,$
$\!{\left| {{z_1} \over {z_2}} \right|} = {{\left| z_1 \right|} \over {\left| z_2 \right|}}, \; si \; {z_2} \ne {0}\,$
${\left| z_1 + z_2 \right|} \le {\left| z_1 \right| + \left| z_2 \right|}\,$ (inégalité triangulaire)
$\!\!{\left| z_1 - z_2 \right|} \ge {\left| {\left| z_1 \right| - \left| z_2 \right|}\right|}\,$
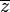$|\overline{z}|=|z|=|-\overline{z}|=|-z|$ .

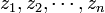(Ici, $\overline{z}$ désigne le conjugué du nombre complexe z. La propriété 6 est une conséquence de l'inégalité triangulaire. L'inégalité triangulaire se généralise à n nombres complexes $z_1, z_2, \cdots, z_n$ ,

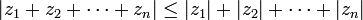$|z_1+z_2+\cdots+z_n|\leq |z_1|+|z_2|+\cdots+|z_n|$ .

Cas d'égalité dans l'inégalité triangulaire : Pour tous nombres complexes z et z', |z+z'|=|z|+|z'| si et seulement si 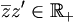$\overline{z}z'\in\mathbb R_+$ , si et seulement s’il existe un réel positif $λ$ tel que $z' = λ z$ ou $z = λ z'$ .

Interprétation géométrique

Article détaillé : Plan d'Argand.

Si on interprète z comme un point dans le plan, c'est-à-dire si on considère son image alors, |z| est la distance de l'image de z à l'origine.

Il est utile d'interpréter l'expression |x - y| comme la distance entre les deux nombres complexes x et y dans le plan complexe.

D'un point de vue algébrique, le module est une valeur absolue, qui confère à l'ensemble des nombres complexes la structure de corps valué. C'est en particulier une norme, de sorte que le plan complexe est un espace vectoriel normé de dimension finie. Il en résulte que c'est aussi un espace métrique (donc un espace topologique).

L'application : 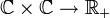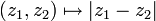$\mathbb C\times \mathbb C \rightarrow \mathbb R_+$ , $(z_1, z_2)\mapsto |z_1-z_2|$ est une distance.

Nombres complexes de module 1

Article détaillé : groupe des unités.

L'ensemble 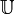$\mathbb U$ des nombres complexes de module 1 est un sous-groupe de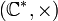 $\left(\mathbb C^*, \times\right)$

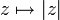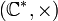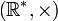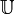L'application $z\mapsto |z|$ de $\left(\mathbb C^*, \times\right)$ dans $\left(\mathbb R^*, \times\right)$ est un morphisme de groupe. Son noyau n'est autre que l'ensemble $\mathbb U$ .

On appelle 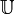$\mathbb U$ le groupe des unités. L'application 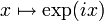$x\mapsto \exp(ix)$ est un morphisme de groupes de R dans U. Ce morphisme est périodique et on note $2π$ sa période. Cette définition du nombre Pi est due au collectif Nicolas Bourbaki^{[réf. nécessaire]}.

Portail des mathématiques

Ce document provient de « Module d%27un nombre complexe ».

Catégorie : Nombre complexe

Wikimedia Foundation. 2010.

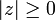
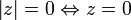
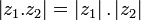
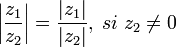
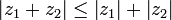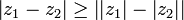
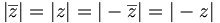Contenu soumis à la licence CC-BY-SA. Source : Article Module (nombres complexes) de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

Nombres complexes — Nombre complexe Pour les articles homonymes, voir complexe. Les nombres complexes forment une extension de l ensemble des nombres réels. Ils permettent notamment de définir des solutions à toutes les équations polynomiales à coefficients réels.… … Wikipédia en Français
Construction nombres complexes — Construction des nombres complexes Il existence différentes constructions du corps des nombres complexes, noté en général C ou . Bien sûr, elles sont toutes équivalentes. Sommaire 1 Constructions purement algébriques 1.1 Définition de Hamilton … Wikipédia en Français
Construction Des Nombres Complexes — Il existence différentes constructions du corps des nombres complexes, noté en général C ou . Bien sûr, elles sont toutes équivalentes. Sommaire 1 Constructions purement algébriques 1.1 Définition de Hamilton … Wikipédia en Français
Construction des nombres complexes — Il existe différentes constructions du corps des nombres complexes, noté en général C ou . Bien sûr, elles sont toutes équivalentes. Sommaire 1 Constructions purement algébriques 1.1 Définition de Hamilton 1.2 Corps … Wikipédia en Français
COMPLEXES (NOMBRES) — Introduits à l’origine comme symboles purement formels destinés à rendre compte des propriétés des équations algébriques, les nombres imaginaires sont d’un usage courant au XVIIIe siècle, mais ce n’est qu’au siècle suivant qu’ils seront définis… … Encyclopédie Universelle
Module D'un Nombre Complexe — Cet article vient en complément à nombre complexe. Le module d un nombre complexe z est un réel positif, noté |z|, qui mesure sa « taille » et généralise la valeur absolue d un nombre réel. En coordonnées cartésiennes, z s écrit a+ib où … Wikipédia en Français
NOMBRES (THÉORIE DES) - Nombres algébriques — Les mathématiciens grecs avaient découvert que certains rapports de grandeurs ne sont pas rationnels, c’est à dire qu’ils ne sont pas égaux au rapport de deux entiers: il en est ainsi du rapport de la diagonale d’un carré à son côté, puisque… … Encyclopédie Universelle
Module Semi-Simple — Camille Jordan, auteur du théorème clé de la théorie En mathématiques et plus particulièrement en algèbre, un A module où A désigne un anneau est qualifié de semi simple ou de complètement réductible si et seulement s il est somme directe de… … Wikipédia en Français
Nombres imaginaires — Nombre complexe Pour les articles homonymes, voir complexe. Les nombres complexes forment une extension de l ensemble des nombres réels. Ils permettent notamment de définir des solutions à toutes les équations polynomiales à coefficients réels.… … Wikipédia en Français
Module d'un nombre complexe — Pour les articles homonymes, voir Module. En mathématiques, le module d un nombre complexe z est un nombre réel positif, noté |z|, qui mesure sa « taille » et généralise la valeur absolue d un nombre réel. En coordonnées cartésiennes, z … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Module (nombres complexes)

Module d'un nombre complexe

Sommaire

Exemples

Propriétés

Interprétation géométrique

Nombres complexes de module 1

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Module (nombres complexes)

Module d'un nombre complexe

Sommaire

Exemples

Propriétés

Interprétation géométrique

Nombres complexes de module 1

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link