- Modulation De Fréquence
-
Modulation de fréquence
Un exemple de modulation de fréquence. En haut, le signal (en rouge) superposé avec la fréquence porteuse (en vert). En bas, le résultat du signal (en bleu) une fois modulé par la fréquence.
La modulation de fréquence ou MF ou FM est un mode de modulation consistant à transmettre un signal par la modulation de la fréquence d'un signal porteur (porteuse).
On parle de modulation de fréquence par opposition à la modulation d'amplitude. En modulation de fréquence, l'information est portée par une modification de la fréquence de la porteuse, et non par une variation d'amplitude. La modulation de fréquence est plus robuste que la modulation d'amplitude pour transmettre un message dans des conditions difficiles (atténuation et bruit importants).
Pour des signaux numériques, on utilise une variante appelée frequency-shift keying ou FSK. La FSK utilise des fréquences discrètes.
Sommaire
Exemples
- les modems (modulateur-demodulateur) bas débit utilisent la modulation de fréquence ;
- les téléphones analogiques utilisent la modulation de fréquence pour composer le numéro : chaque chiffre est codé par une combinaison de deux fréquences pour former un code DTMF. Il s'agit d'une modulation FSK qui utilise plus de deux fréquences (MFSK, multiple frequency-shift keying) ;
- les radios de la « bande FM » émettent, comme leur nom l'indique, en modulation de fréquence sur la bande VHF II.
Théorie
On suppose que le signal à transmettre est :
avec la restriction suivante sur l'amplitude :
La porteuse sinusoïdale est :
où fp est la fréquence de la porteuse en hertz et A une amplitude arbitraire. Le signal modulé en FM est le suivant :
- où f(t) = fp + fΔxm(t)
Dans cette équation, f(t) est la fréquence instantanée de l'oscillateur et fΔ la déviation en fréquence, qui correspond à la déviation maximale par rapport à la fréquence de la porteuse fp, en supposant que xm(t) est limité à l'intervale [-1; +1].
Bien qu'à première vue on puisse imaginer que les fréquences soient limitées à l'intervalle fp ± fΔ, ce raisonnement néglige la distinction entre fréquence instantanée et fréquence spectrale. Le spectre harmonique d'un signal FM réel possède des composantes qui vont jusqu'à des fréquences infinies, bien qu'elles deviennent rapidement négligeables.
De façon simplifiée, le spectre d'une porteuse sinusoïdale modulée en FM par un signal sinusoïdal peut être représenté par une fonction de Bessel, ce qui permet de modéliser formellement l'occupation spectrale d'une modulation FM.
De façon approchée, la règle de Carson indique qu'à peu près toute la puissance (~98%) d'un signal modulé en fréquence est comprise dans la bande de fréquences :
où fΔ est la déviation maximale de la fréquence instantanée f(t) à partir de la fréquence de la porteuse fp (en supposant que xm(t) est dans l'intervalle [-1; +1]), et fm est la plus grande fréquence du signal à transmettre xm(t).
Note : la modulation de fréquence peut être vue comme un cas particulier de la modulation de phase où la modulation en phase de la porteuse est l'intégrale temporelle du signal à transmettre.
Dans l'usage courant, la fréquence de modulation est toujours inférieure à la fréquence porteuse, mais ne pas suivre cette règle peut donner des résultats intéressants, notamment en synthèse sonore.
Cas d'un signal sinusoïdal
La modulation d'une porteuse sinusoïdale par un signal sinusoïdal de fréquence moindre peut s'écrire ainsi :
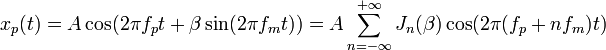
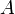: amplitude du signal
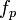: fréquence porteuse
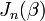: fonction de Bessel de première espèce
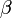: indice de modulation
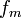: fréquence de modulation
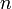: rang harmonique de fm,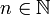 
En faisant varier β, on fait varier l'intensité de la modulation, donc l'écart entre la fréquence la plus grande et la plus petite, qui alternent à la fréquence fm.
Cas de la FSK
En FSK, le signal xm peut prendre un ensemble de valeurs discrètes xi (par exemple deux dans les modulations binaires), ce qui donne pendant la transmission d'une valeur xi :
On voit ainsi que la fréquence instantanée ne peut prendre qu'un ensemble discret de valeurs, une valeur pour chaque valeur xi du signal à transmettre.
Voir aussi
Portail de l’électricité et de l’électronique
Catégorie : Modulation analogique du signal
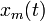
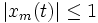
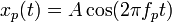
![x_t(t) = A \cos \left( 2 \pi \int_{0}^{t} f(\tau)\, d \tau \right) = A \cos \left( 2 \pi \int_{0}^{t} \left[ f_p + f_\Delta x_m(\tau) \right] \, d \tau \right)](/pictures/frwiki/100/d5ee3dea1a82e96143beb746041ae076.png)
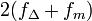
![x_p(t) = A \cos \left( 2 \pi \int_{0}^{t} \left[ f_p + f_\Delta x_i \right] \, d \tau \right) = A \cos \left( 2 \pi \left[ f_p + f_\Delta x_i \right] t \right)](/pictures/frwiki/48/0e8457ac868bada0ada546cfa93968de.png)
Wikimedia Foundation. 2010.
