Miroir de bragg

Le miroir de Bragg, mis au point par William Lawrence Bragg (prix Nobel de physique en 1915), est une succession de surfaces planes transparentes d’indices de réfraction différents. Il permet de réfléchir, grâce à des phénomènes d’interférences constructives, 99,5 % de l’énergie incidente. Ceci est possible à condition que l’onde incidente soit proche de l’incidence normale. Aucun autre miroir ne peut égaler ce résultat (les pertes diélectriques étant plus faibles que les pertes métalliques pour les longueurs d’ondes optiques).

Sommaire 1 Principe 2 Applications 3 Voir aussi 3.1 Articles connexes

Principe

Une structure simple de miroir de Bragg est un empilement de plusieurs couches d’indices optiques différents. Si l'on considère deux matériaux, l’un d’indice de réfraction faible n₁, l’autre d’indice plus fort n₂, la réflectivité maximale est obtenue pour la longueur d’onde dite de Bragg λ_Bragg si les épaisseurs sont fixées à 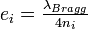pour chaque couche d'indice n_i.

En effet, pour ces épaisseurs précises, le déphasage subi par une onde ayant parcouru l’épaisseur optique , est exactement égal à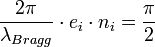

Un miroir de Bragg est donc construit pour une longueur d'onde donnée et une température donnée, l'épaisseur variant avec celle-ci.

Considérons les deux milieux 1 et 2, non absorbants, tels que n₁ < n₂ et agencés selon un empilement 1|2|1|2|… L’intérêt du miroir de Bragg se base sur les propriétés suivantes :

• Pour une onde se propageant d’un milieu d’indice fort vers celui d’indice plus faible, la réflexion à l’interface n’induit pas de déphasage.
• Pour une onde se propageant d’un milieu d’indice faible vers celui d’indice plus fort, la réflexion à l’interface induit un déphasage de π.

Soient r un rayon qui parcourt cet empilement, et r₁, r₂, r₃,... les rayons réfléchis sur chaque interface. Prenons les réflexions aux deux premières interfaces:

• Par exemple pour r2, à la fin de son double parcours (aller - réflexion sur 2|1 - retour) dans le milieu 2, le déphasage vaut :
• Or pour r1, juste après la réflexion, le déphasage vaut également π.

Par conséquent, les rayons sont en phase (orange et rouge sur la figure).

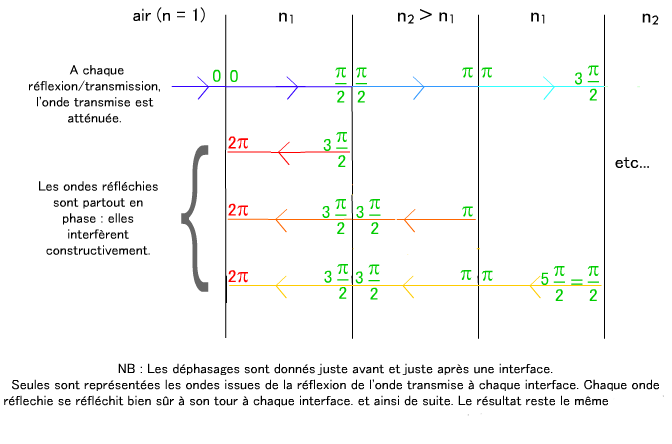
Figure : Principe du miroir de Bragg

Il en va de même dans le cas de r2 et r3, où les déphasages sont respectivement 0 et 2π. Ainsi tous les rayons réfléchis sont en phase, impliquant des interférences constructives c'est à dire une sommation des amplitudes. Ainsi l’augmentation du nombre de paire de couches accroît la réflectivité du miroir en réinjectant chaque fois une partie de l’intensité transmise.

Applications

La question de la réflectivité d'un matériau est très importante dans le domaine des lasers. La nécessité d’améliorer l’efficacité des cavités optiques des lasers, particulièrement pour les diodes lasers, a conduit à s’intéresser à l’amélioration des parois réflectives de ces cavités. En effet, pour optimiser l’interaction d’une onde avec le milieu amplificateur, on renvoie l’onde plusieurs fois dans ce milieu à l’aide de réflecteurs (miroirs). Le milieu amplificateur est placé dans une cavité dont les parois doivent être les plus réfléchissantes possibles, afin d’augmenter considérablement la puissance réinjectée dans ce même milieu, compenser les pertes et produire un faisceau. C’est le principe de la cavité laser. Le problème pour la réduction des dimensions des cavités est biensûr la taille du milieu amplificateur. Le miroir de Bragg est alors utilisé pour obtenir une excellente réflectivité permettant ainsi, pour une efficacité de cavité similaire, la réduction de la taille du milieu amplificateur.

Voir aussi

• Réseau de Bragg

Articles connexes

• William Lawrence Bragg
• indice de réfraction
• interférence
• Cavité optique

• Portail de la physique