Mesure algebrique

Mesure algebrique

Mesure algébrique

Page d'aide sur l'homonymie Pour les articles homonymes, voir mesure.

En géométrie élémentaire

En géométrie, une mesure algébrique est une longueur affectée d'un signe, ce qui permet d'en orienter le sens sur un axe donné.

Ainsi, alors que la longueur d'un segment est toujours positive, on peut utiliser une mesure algébrique de ce segment, qui sera égale à sa longueur si on la prend dans un sens, et à l'opposé de sa longueur si on la prend dans l'autre.

La notation qui différencie une mesure algébrique relative à un segment de la longueur de celui-ci consiste à placer une barre horizontale au-dessus des lettres qui représentent les deux points du segment. Alors que l'ordre des lettres n'a pas d'importance dans la notation d'une longueur, il définit justement le signe de la mesure algébrique, puisque la première lettre désigne le point de départ et la seconde désigne le point d'arrivée.

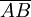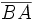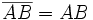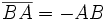Exemple : pour un segment AB (ou BA, ce qui est équivalent), la mesure algébrique peut être \overline{AB} ou \overline{BA}. Si l'on suppose que l'axe est orienté de A vers B, alors \overline{AB} = AB et \overline{BA} = -AB, et inversement.

En géométrie affine

La notion de mesure algébrique apparaît dans certains énoncés de résultats (théorème de Thalès, théorème de Ceva, théorème de Ménélaüs) qui ne nécessitent nullement que soit définie une unité de « longueur », ni même que l'espace où l'on travaille soit fondé sur le corps des réels.

En premier lieu, étant donnés deux points A et B d'un espace affine, il est possible de définir[1] la mesure algébrique 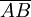\overline{AB} dès lors qu'on a préalablement privilégié un vecteur 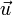\vec u parmi ceux dirigeant la droite (AB) : la notation 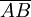\overline{AB} désignera simplement l'unique scalaire λ tel que 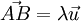\vec{AB}=\lambda \vec u. Ceci généralise bien la définition « naïve » : si on est sur une droite orientée dans un espace affine euclidien, on retrouve la même quantité que plus haut si on prend pour 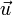\vec u le vecteur unitaire orientant (AB) et pointant dans le sens indiqué par l'orientation.

Plus spécifiquement, lorsqu'interviennent des rapports de mesures algébriques, il n'est plus besoin de disposer d'un vecteur de référence. Étant donnés trois points alignés A, B et C d'un espace affine (et rien d'autre), tels que 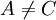A\not=C, on peut définir[2] la quantité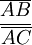

{\overline{AB}\over\overline{AC}}

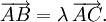
comme l'unique scalaire λ tel que \overrightarrow{AB}=\lambda\,\overrightarrow{AC}.

Notes et références

  1. ↑ Cette définition est par exemple disponible dans le cours de Mathématiques de L. Lesieur et C. Joulain, Armand Colin, 1966, tome I, p. 223.
  2. ↑ Voir par exemple la note 2.4.6 dans le traité de Géométrie de Marcel Berger (tome 1, p. 68 dans l'édition de 1979 - CEDIC Fernand Nathan). Marcel Berger note ce scalaire 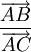{\overrightarrow{AB}\over\overrightarrow{AC}}, ce qui souligne que cette notion de « rapport » prend son sens indépendamment de celle de mesure algébrique. On peut d'ailleurs remarquer que la langue allemande donne un nom à ce rapport (« Teilverhältnis ») pour lequel existe une notation spécifique (TV(B,C,A)) - voir par exemple (de) un aide-mémoire de géométrie affine de Bernard Kabelka, disponible en ligne sur le site de l'univsrsité technique de Vienne (consulté le 30 septembre 2007).
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Mesure alg%C3%A9brique ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Mesure algebrique de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Mesure Algébrique — Pour les articles homonymes, voir mesure. En géométrie élémentaire En géométrie, une mesure algébrique est une longueur affectée d un signe, ce qui permet d en orienter le sens sur un axe donné. Ainsi, alors que la longueur d un segment est… …   Wikipédia en Français

  • Mesure algébrique — Pour les articles homonymes, voir mesure. En géométrie élémentaire En géométrie, une mesure algébrique est une longueur affectée d un signe, ce qui permet d en orienter le sens sur un axe donné. Ainsi, alors que la longueur d un segment est… …   Wikipédia en Français

  • algébrique — [ alʒebrik ] adj. • XVIIIe; algébraïque 1585; de algèbre ♦ Relatif à l algèbre, qui s effectue par l algèbre. Calcul numérique et calcul algébrique. Mesure, quantité algébrique. Courbe, équation, fonction algébrique. Nombre algébrique. Topologie… …   Encyclopédie Universelle

  • Algebrique — Algébrique Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom …   Wikipédia en Français

  • MESURE — DÈS qu’un phénomène d’apparence bien définie est justiciable d’une quantification, de manière répétable et suffisamment précise, il est considéré comme une grandeur . On peut caractériser son état ou son intensité par un nombre ou valeur et faire …   Encyclopédie Universelle

  • Algébrique — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « Algébrique », sur le Wiktionnaire (dictionnaire universel) Courbe algébrique Clôture algébrique Type… …   Wikipédia en Français

  • Mesure — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « Mesure », sur le Wiktionnaire (dictionnaire universel) En musique, la mesure est une unité temporelle… …   Wikipédia en Français

  • Longueur algébrique — Mesure algébrique Pour les articles homonymes, voir mesure. En géométrie élémentaire En géométrie, une mesure algébrique est une longueur affectée d un signe, ce qui permet d en orienter le sens sur un axe donné. Ainsi, alors que la longueur d un …   Wikipédia en Français

  • Expression algébrique — Algèbre L algèbre est la branche des mathématiques qui étudie, d une façon générale, les structures algébriques. L étude des structures algébriques peut être faite de manière unifiée dans la cadre de l algèbre universelle. L étude épistémologique …   Wikipédia en Français

  • Langage algébrique — En théorie des langages formels, un langage algébrique ou langage non contextuel est un langage qui peut être engendré par une grammaire algébrique. De manière équivalente un langage algébrique est un langage reconnu par automate à pile. Les… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”