Loi de distribution des vitesses de maxwell

Loi de distribution des vitesses de maxwell

Loi de distribution des vitesses de Maxwell

En théorie cinétique des gaz, la loi de distribution de vitesses de Maxwell donne la densité de probabilité d'observer, dans un gaz à l'équilibre thermodynamique global à la température T uniforme, un atome dont le vecteur vitesse soit \vec{v}. Elle est nommée suivant le physicien écossais James Clerk Maxwell. La loi de distribution de Maxwell s'écrit :

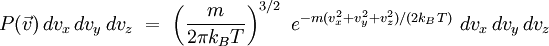
P(\vec{v}) \, dv_x \, dv_y \, dv_z \ = \ \left(\frac{m}{2\pi k_B T}\right)^{3/2} \ e^{-m(v_x^2+v_y^2+v_z^2)/(2k_B T)} \ dv_x \, dv_y \, dv_z

Sommaire

Dérivation élémentaire

On considère un gaz parfait à l'équilibre thermodynamique global. En supposant que la distribution des vitesses est isotrope (pas de direction privilégiée), la densité de probabilité du gaz ne peut dépendre que de la norme du vecteur vitesse. Donc on peut écrire :

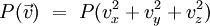
P(\vec{v}) \ = \ P(v_x^2+v_y^2+v_z^2)

D'autre part, si on suppose que les composantes vx,vy,vz sont des variables aléatoires indépendantes (ce qui est une hypothèse de "désordre" maximal ou plus précisément d'entropie maximale), on doit aussi avoir :

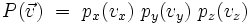
P(\vec{v}) \ = \ p_x(v_x) \ p_y(v_y) \ p_z(v_z)

Par isotropie, les trois fonctions pi doivent de plus être identiques :

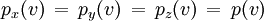
p_x(v) \, = \, p_y(v) \, = \, p_z(v) \, = \, p(v)

On en déduit que :

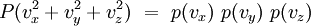
P(v_x^2+v_y^2+v_z^2) \ = \ p(v_x) \ p(v_y) \ p(v_z)

En faisant vy = vz = 0, on obtient :

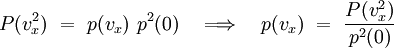
P(v_x^2) \ = \ p(v_x) \ p^2(0) \quad \Longrightarrow \quad p(v_x)\ = \ \frac{P(v_x^2) }{p^2(0)}

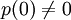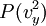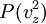où l'on a supposé p(0) \ne 0. On obtient des relations analogues pour P(v_y^2) et P(v_z^2), à partir desquelles on peut écrire :

P(v_x^2+v_y^2+v_z^2) \ = \ p(v_x) \ p(v_y) \ p(v_z) \ = \ \frac{1}{p^6(0)} \ \left[ \ P(v_x^2) \ P(v_y^2) \ P(v_z^2) \ \right]

Cette équation fonctionnelle pour la fonction inconnue P admet une solution unique :

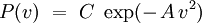
P(v) \ = \ C \ \exp(- \, A \, v^2)

où C et A sont deux constantes.

Autres dérivations

  • La distribution de Maxwell peut se déduire des lois générales de la physique statistique d'équilibre, comme application du facteur de Boltzmann.
  • Elle peut aussi être obtenue comme l'unique solution stationnaire de l'équation de Boltzmann décrivant un gaz hors d'équilibre.

Voir aussi

Articles connexes

  • Portail de la physique Portail de la physique
Ce document provient de « Loi de distribution des vitesses de Maxwell ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Loi de distribution des vitesses de maxwell de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Loi De Distribution Des Vitesses De Maxwell — En théorie cinétique des gaz, la loi de distribution de vitesses de Maxwell donne la densité de probabilité d observer, dans un gaz à l équilibre thermodynamique global à la température T uniforme, un atome dont le vecteur vitesse soit . Elle est …   Wikipédia en Français

  • Loi de distribution des vitesses de Maxwell — En théorie cinétique des gaz, la loi de distribution de vitesses de Maxwell donne la densité de probabilité d observer, dans un gaz à l équilibre thermodynamique global à la température T uniforme, un atome dont le vecteur vitesse soit . Elle est …   Wikipédia en Français

  • Loi scientifique — Liste des lois scientifiques Liste des lois scientifiques par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom de la loi comprend des noms de scientifiques, on se base sur le premier… …   Wikipédia en Français

  • MAXWELL (J. C.) — L’œuvre du savant britannique Maxwell a été capitale pour la théorie physique. Elle a permis d’obtenir une connaissance unifiée des phénomènes lumineux et électromagnétiques, ce qui est d’autant plus remarquable que cette unification se situe… …   Encyclopédie Universelle

  • Liste Des Lois Scientifiques — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom de la loi comprend des noms de scientifiques, on se base sur le premier nom propre cité. Si le nom de la loi ne comprend pas de… …   Wikipédia en Français

  • Liste des lois scientifiques — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom de la loi comprend des noms de scientifiques, on se base sur le premier nom propre cité. Si le nom de la loi ne comprend pas de… …   Wikipédia en Français

  • Loi De Biot Et Savart — La loi de Biot et Savart, nommé en l honneur des physicien français Jean Baptiste Biot et Félix Savart (1820) donne le champ magnétique créé par une distribution de courants continus. Elle constitue l une des lois fondamentales de la… …   Wikipédia en Français

  • Loi de Biot-Savart — Loi de Biot et Savart La loi de Biot et Savart, nommé en l honneur des physicien français Jean Baptiste Biot et Félix Savart (1820) donne le champ magnétique créé par une distribution de courants continus. Elle constitue l une des lois… …   Wikipédia en Français

  • Loi de biot et savart — La loi de Biot et Savart, nommé en l honneur des physicien français Jean Baptiste Biot et Félix Savart (1820) donne le champ magnétique créé par une distribution de courants continus. Elle constitue l une des lois fondamentales de la… …   Wikipédia en Français

  • Histoire de la termodynamique, de la mécanique statistique, et des processus aléatoires — Chronologie de la thermodynamique et de la physique statistique Sadi Carnot, pionnier de la thermodynamique. Article principal : Histoire de la thermodynamique classique. Cet article présente une frise chronologique des évènements notables… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”