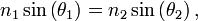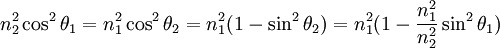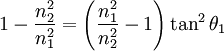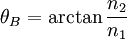Angle de brewster

Angle de Brewster

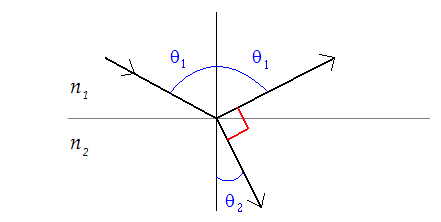
Lorsque l'on envoie un faisceau lumineux sur un dioptre, on observe en général une réflexion partielle. Si le faisceau est incliné d'un angle nommé angle de Brewster, la réflexion partielle disparait, à condition que la lumière soit polarisée dans le plan d'incidence (polarisation dite p ou TM). À l'angle de Brewster, le rayon réfracté et la direction attendue pour le rayon réfléchi forment un angle droit.

La formule de Snell-Descartes permet de prévoir facilement l'angle de Brewster si l'on connait les indices de réfraction $n 1$ et $n 2$ des milieux. Écrivant

$n_1 \sin \left( \theta_1 \right) =n_2 \sin \left( \theta_2 \right),$

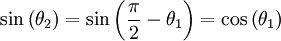$\sin \left( \theta_2 \right) = \sin \left( \frac{\pi}{2} - \theta_1 \right)=\cos \left( \theta_1 \right)$ ,

on obtient :

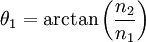$\theta_1 = \arctan \left( \frac{n_2}{n_1} \right)$ .

Interprétation physique

L'onde réfléchie dans le milieu 1 trouve son origine dans l'oscillation des charges dans le milieu 2. Comme l'oscillation est perpendiculaire à l'onde réfractée, elle se retrouve, dans le cas particulier d'une onde TM à l'angle de Brewster, avoir lieu dans la direction même de l'onde réfléchie, rendant l'excitation de celle-ci impossible.

Applications

Dans les lasers dont le milieu amplificateur est séparé des miroirs de cavité, les dioptres délimitant ce milieu sont inclinés à l'angle de Brewster pour éliminer les pertes par réflexion partielle.

Les lunettes polarisantes polarisées verticalement permettent de supprimer la lumière naturelle réfléchie sur des surfaces horizontales à l'angle de Brewster. Elles permettent d'atténuer fortement les réflexions parasites voisines de cet angle.

Calcul à partir des formules de Fresnel

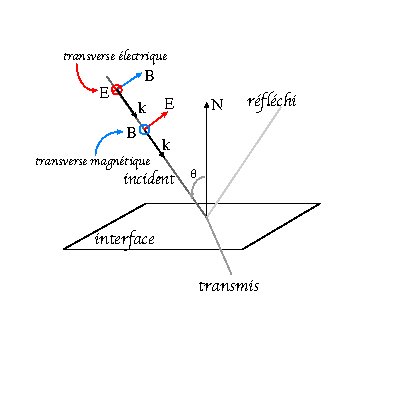
géométrie et polarisations de la lumière à une interface

Les lois de la réflexion-transmission (lois de Snell-Descartes) portent sur les directions des rayons réfléchis et transmis, mais le comportement des ondes TE et TM diffère en ce qui concerne les intensités respectives des ondes réfléchies et transmises (cf. les coefficients de Fresnel). Ces intensités varient avec l'angle d'incidence. À une incidence égale à l'angle de Brewster $θ b$ , l'onde TM est totalement transmise et le rayon réfléchi disparait.

Démonstration

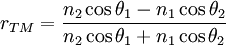
Le coefficient de Fresnel en réflexion pour une onde polarisée TM s'écrit $r_{TM} = \frac{n_{2} \cos \theta_{1} - n_{1} \cos \theta_{2}}{n_{2} \cos \theta_{1} + n_{1} \cos \theta_{2}}$

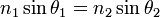
où les angles $θ 1$ et $θ 2$ sont liés par la loi de Snell-Descartes : $\quad n_{1} \sin \theta_{1} = n_{2} \sin \theta_{2}$

Pour annuler le numérateur du coefficient en réflexion, on doit donc avoir

$n_2^2 \cos^2 \theta_1 = n_1^2 \cos^2 \theta_2 = n_1^2 ( 1 - \sin^2 \theta_2 ) = n_1^2 (1 - \frac{n_1^2}{n_2^2} \sin^2 \theta_1)$

En divisant le membre de gauche et celui de droite par 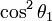$\quad \cos^2 \theta_1$ et en remarquant que 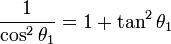$\frac{1}{\cos^2 \theta_1} = 1 + \tan^2 \theta_1$ , on obtient

$\quad 1 - \frac{n_2^2}{n_1^2} = \left( \frac{n_1^2}{n_2^2} - 1 \right) \tan^2 \theta_1$

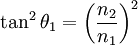
c'est-à-dire $\tan^2 \theta_1 = \left( \frac{n_2}{n_1} \right)^2$

L'angle de Brewster étant, par définition, la valeur de l'angle d'incidence $θ 1$ telle que le coefficient de réflexion de la composante TM de l'onde soit nul, on retrouve bien

$\theta_B = \arctan \frac{n_2}{n_1}$

Portail de la physique

Ce document provient de « Angle de Brewster ».

Catégorie : Optique géométrique

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Angle de brewster de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

Angle De Brewster — Lorsque l on envoie un faisceau lumineux sur un dioptre, on observe en général une réflexion partielle. Si le faisceau est incliné d un angle nommé angle de Brewster, la réflexion partielle disparait, à condition que la lumière soit polarisée… … Wikipédia en Français
Angle de Brewster — Lorsque l on envoie un faisceau lumineux sur un dioptre, on observe en général une réflexion partielle. Si le faisceau est incliné d un angle nommé angle de Brewster, la réflexion partielle disparait, à condition que la lumière soit polarisée… … Wikipédia en Français
angle de Brewster — Briusterio kampas statusas T sritis fizika atitikmenys: angl. Brewster angle vok. Brewsterscher Winkel, m; Brewster Winkel, m rus. угол Брюстера, m pranc. angle de Brewster, m … Fizikos terminų žodynas
Brewster (homonymie) — Brewster Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Brewster peut faire référence à : Personnes Brewster Kahle, un informaticien, fondateur d Alexa et d Internet Archive, Brewster H. Shaw, un… … Wikipédia en Français
Brewster angle — Briusterio kampas statusas T sritis fizika atitikmenys: angl. Brewster angle vok. Brewsterscher Winkel, m; Brewster Winkel, m rus. угол Брюстера, m pranc. angle de Brewster, m … Fizikos terminų žodynas
Brewster — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Brewster peut faire référence à : Personnes Brewster Kahle, un informaticien, fondateur d Alexa et d Internet Archive, Brewster H. Shaw, un… … Wikipédia en Français
Brewster-Winkel — Briusterio kampas statusas T sritis fizika atitikmenys: angl. Brewster angle vok. Brewsterscher Winkel, m; Brewster Winkel, m rus. угол Брюстера, m pranc. angle de Brewster, m … Fizikos terminų žodynas
Angle (homonymie) — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Angle Géométrie Angle d or Angle diédral Angles opposés par le sommet Angles supplémentaires Angle droit Angle plan Angle rentrant Angle solide Angles… … Wikipédia en Français
Brewster — may refer to:People* Anna Brewster * Benjamin Brewster * Benjamin H. Brewster, American attorney, cabinet member * Craig Brewster * Daniel Brewster * David Brewster, Scottish scientist * Diane Brewster * Elizabeth Brewster * Harlan Carey Brewster … Wikipedia
Brewster Angle Microscopy — Brewster Angle Microscopy Микроскопия угла Брюстера (микроскопия под углом Брюстера) Разновидность оптической микроскопии, в которой для формирования изображения используется линейно поляризованное излучение, падающее на отражающую… … Толковый англо-русский словарь по нанотехнологии. - М.

Dictionnaires et Encyclopédies sur 'Academic'

Angle de brewster