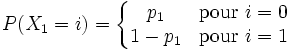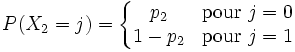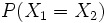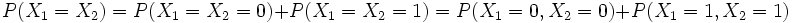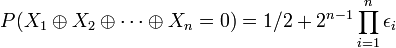Lemme piling-up

Lemme piling-up

Lemme Piling-Up

Le lemme Piling-Up est un résultat statistique introduit par Mitsuru Matsui en 1993 dans le cadre de la cryptanalyse linéaire. Ce lemme permet de quantifier le biais statistique présent dans une approximation linéaire d'un algorithme de chiffrement symétrique par bloc.

Formulation mathématique

Une équation linéaire dans le cadre de la cryptanalyse linéaire se présente sous la forme d'un ou-exclusif de variables binaires :

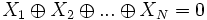
X_1 \oplus X_2 \oplus ... \oplus X_N = 0

Soit 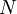N~ variables aléatoires, indépendantes et binaires (le résultat de l'événement est soit 0, soit 1), 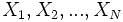X_1, X_2, ..., X_N~, la probabilité que cette équation soit correcte est :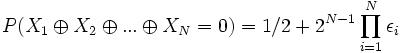

P(X_1 \oplus X_2 \oplus ... \oplus X_N = 0) = 1/2 + 2^{N-1}\prod_{i=1}^{N}\epsilon_i

avec 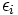\epsilon_i~, le biais linéaire de la variable aléatoire 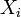X_i~. Ce biais peut être positif ou négatif et quantifie l'écart par rapport à une distribution uniforme où l'espérance d'une variable aléatoire binaire est 1/2. Plus le biais est important, plus un algorithme de chiffrement est susceptible d'être attaqué via la cryptanalyse linéaire.

Raisonnement

Soit 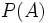P(A)~, la probabilité que l'événement A arrive. Avec une probabilité de 1, l'événement se produira. Inversement, une probabilité de 0 indique l'impossibilité de cet événement. Dans le cadre du lemme Piling-Up, nous avons donc affaire à des variables aléatoires, binaires et considérées comme indépendantes.

Considérons d'abord le lemme pour deux variables aléatoires :

P(X_1 = i)=\left\lbrace\begin{matrix}p_1 & \hbox{pour }i=0 \\ 1-p_1 & \hbox{pour }i=1\end{matrix}\right.
P(X_2 = j)=\left\lbrace\begin{matrix}p_2 & \hbox{pour }j=0 \\ 1-p_2 & \hbox{pour }j=1\end{matrix}\right.

Considérons maintenant la probabilité d'une équation linéaire avec ces deux variables :

P(X_1 \oplus X_2 = 0)

Grâce aux propriétés de XOR, ceci est équivalent à :

P(X_1=X_2)~

X1 = X2 = 0 et X1 = X2 = 1 sont des événements mutuellement exclus et de ce fait :

P(X_1=X_2)=P(X_1=X_2=0) + P(X_1=X_2=1)=P(X_1=0, X_2=0) + P(X_1=1, X_2=1)~


Nous partons dès lors du principe que les variables sont indépendantes. C’est-à-dire que l'état d'une variable ne va pas influencer l'état d'une autre. On peut ainsi étendre la probabilité au résultat suivant :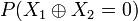

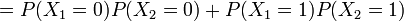
P(X_1 \oplus X_2 = 0) =P(X_1=0)P(X_2=0)+P(X_1=1)P(X_2=1)\
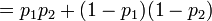
=p_1p_2 + (1-p_1)(1-p_2)\
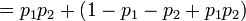
=p_1p_2 + (1-p_1-p_2+p_1p_2)\
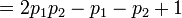
=2p_1p_2-p_1-p_2+1\

Nous exprimons maintenant les probabilités p1 et p2 comme ½ + ε1 et ½ + ε2, où les ε sont des biais de probabilités — la quantité de déviation de la probabilité par rapport à ½.

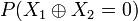
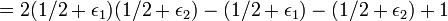
P(X_1 \oplus X_2 = 0) =2(1/2+\epsilon_1)(1/2+\epsilon_2)-(1/2+\epsilon_1)-(1/2+\epsilon_2)+1\
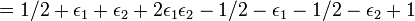
=1/2+\epsilon_1+\epsilon_2+2\epsilon_1\epsilon_2-1/2-\epsilon_1-1/2-\epsilon_2+1\
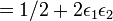
=1/2+2\epsilon_1\epsilon_2\

Ainsi, le biais ε1,2 pour la somme de XOR ci-dessus est de 2ε1ε2.

Cette formule peut s'étendre pour un nombre infini de variables comme suit :

P(X_1\oplus X_2\oplus\cdots\oplus X_n=0)=1/2+2^{n-1}\prod_{i=1}^n \epsilon_i

Si un ε est à zéro, c’est-à-dire qu'une des variables est non-biaisée, alors l'ensemble de la fonction ne sera pas biaisée et égale à ½.

Voir aussi

  • Portail de la cryptologie Portail de la cryptologie
Ce document provient de « Lemme Piling-Up ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Lemme piling-up de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

  • Lemme Piling-Up — Le lemme Piling Up est un résultat statistique introduit par Mitsuru Matsui en 1993 dans le cadre de la cryptanalyse linéaire. Ce lemme permet de quantifier le biais statistique présent dans une approximation linéaire d un algorithme de… …   Wikipédia en Français

  • Liste des lemmes (mathematiques) — Liste des lemmes (mathématiques) Liste des lemmes mathématiques par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom des lemmes comprend des noms de scientifiques, on se base sur le… …   Wikipédia en Français

  • Liste des lemmes (mathématiques) — Liste des lemmes mathématiques par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom des lemmes comprend des noms de scientifiques, on se base sur le premier nom propre cité. Si le nom …   Wikipédia en Français

  • Liste de lemmes (mathématiques) — Liste de lemmes mathématiques par ordre alphabétique. En mathématiques, un lemme est un énoncé prouvé, mais jugé moins important que ce qu on appelle un théorème, qu il sert généralement à établir au cours d une démonstration. Néanmoins cette… …   Wikipédia en Français

  • 3-Way — Pour les articles homonymes, voir Way. 3 Way Résumé Concepteur(s) Joan Daemen Première publication 1994 Dérivé de Aucun …   Wikipédia en Français

  • 3DES — Triple DES Triple DES 3DES avec ses trois opérations DES Résumé …   Wikipédia en Français

  • 3 Way — [[Image:|none|240px]] Résumé Concepteur(s) Joan Daemen Première publication …   Wikipédia en Français

  • A5/3 — Kasumi (chiffrement) Pour les articles homonymes, voir Kasumi. KASUMI …   Wikipédia en Français

  • AES-128 — Advanced Encryption Standard process Le Advanced Encryption Standard process est un processus de standardisation lancé par le NIST en 1997 pour demander aux cryptologues de concevoir un nouvel algorithme de chiffrement par bloc destiné au… …   Wikipédia en Français

  • AES-256 — Standard de chiffrement avancé Pour les articles homonymes, voir AES. AES …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”