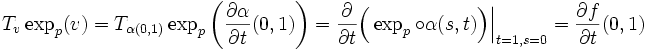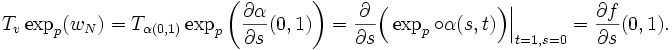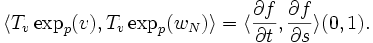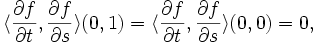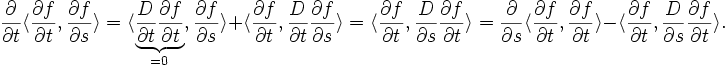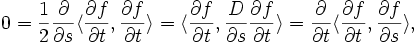- Lemme de Gauss (géométrie Riemannienne)
-
Lemme de Gauss (géométrie Riemannienne)
Dans la géométrie Riemannienne, le lemme de Gauss permet de comprendre l'application exponentielle comme une isométrie radiale. Dans ce qui suit, soit M une variété de Riemann dotée d'une connexion de Levi-Civita (i.e. en particulier, cette connexion est symétrique et compatible avec la métrique de M).
Sommaire
Introduction
Nous avons défini sur M l'application exponentielle en
 par
paroù on a dû restreindre le domaine TpM de définition à une boule Bε(0) de rayon ε > 0 et de centre 0 pour s'assurer que expp est bien définie et où γ(1,p,v) est le point
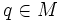 atteint en suivant l'unique géodésique γ passant par le point
atteint en suivant l'unique géodésique γ passant par le point  avec la vitesse
avec la vitesse 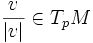 sur une distance
sur une distance 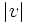 . Nous remarquons très aisément que expp est un difféomorphisme local autour de
. Nous remarquons très aisément que expp est un difféomorphisme local autour de 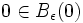 . En effet, soit
. En effet, soit  une courbe différentiable dans TpM telle que α(0): = 0 et α'(0): = v. Comme
une courbe différentiable dans TpM telle que α(0): = 0 et α'(0): = v. Comme 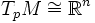 , il est clair qu'on peut choisir α(t): = vt. Dans ce cas, par la définition de la différentielle de l'exponentielle en 0 appliquée sur v, nous obtenons
, il est clair qu'on peut choisir α(t): = vt. Dans ce cas, par la définition de la différentielle de l'exponentielle en 0 appliquée sur v, nous obtenonsLe fait que expp soit un difféomorphisme local et que T0expp(v) = v pour tout
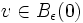 nous permet d'affirmer que expp est une isométrie locale autour de 0, i.e.
nous permet d'affirmer que expp est une isométrie locale autour de 0, i.e.Ceci signifie en particulier qu'il est possible d'identifier la boule
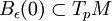 avec un petit voisinage autour de
avec un petit voisinage autour de  . Nous sommes déjà contents de voir que expp est une isométrie locale, mais on aimerait bien que ce soit un peu plus que ça. Il s'avère qu'il est en fait possible de montrer que cette application est même une isométrie radiale !Fichier:Gauss lemma local isometry.pngL'exponentielle comme isométrie locale
. Nous sommes déjà contents de voir que expp est une isométrie locale, mais on aimerait bien que ce soit un peu plus que ça. Il s'avère qu'il est en fait possible de montrer que cette application est même une isométrie radiale !Fichier:Gauss lemma local isometry.pngL'exponentielle comme isométrie localeCeci signifie en particulier qu'il est possible d'identifier la boule
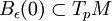 avec un petit voisinage autour de
avec un petit voisinage autour de  . Nous sommes déjà contents de voir que
. Nous sommes déjà contents de voir que 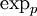 est une isométrie locale, mais on aimerait bien que ce soit un peu plus que ça. Il s'avère qu'il est en fait possible de montrer que cette application est même une isométrie radiale !
est une isométrie locale, mais on aimerait bien que ce soit un peu plus que ça. Il s'avère qu'il est en fait possible de montrer que cette application est même une isométrie radiale !Lemme de Gauss : l'exponentielle comme isométrie radiale
Soit
 . Dans ce qui suit, nous faisons l'identification
. Dans ce qui suit, nous faisons l'identification 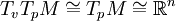 . Le lemme de Gauss dit :
. Le lemme de Gauss dit :Soient
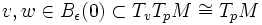 et
et 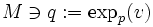 . Alors,
. Alors,Pour
 , ce lemme signifie que
, ce lemme signifie que 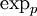 est une isométrie radiale dans le sens suivant : soit
est une isométrie radiale dans le sens suivant : soit 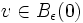 , i.e. tel que
, i.e. tel que 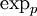 est bien définie. De plus, soit
est bien définie. De plus, soit  . Alors, l'exponentielle
. Alors, l'exponentielle 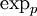 reste une isométrie en
reste une isométrie en 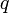 , et, plus généralement, tout au long de la géodésique
, et, plus généralement, tout au long de la géodésique 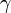 (pour autant que
(pour autant que  soit bien définie) ! Donc, radialement, dans toutes les directions permises par le domaine de définition de
soit bien définie) ! Donc, radialement, dans toutes les directions permises par le domaine de définition de 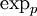 , celle-ci reste une isométrie.Fichier:Gauss lemma radial isometry.pngL'exponentielle comme isométrie radiale
, celle-ci reste une isométrie.Fichier:Gauss lemma radial isometry.pngL'exponentielle comme isométrie radialePreuve
Rappelons que
Nous procédons en trois étapes :
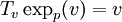 : construisons une courbe
: construisons une courbe 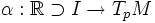 telle que
telle que 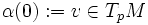 ,
,  et | v | = cste. Comme
et | v | = cste. Comme 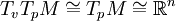 , on peut poser
, on peut poser 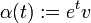 . Alors,
. Alors,
Calculons maintenant le produit scalaire
 .
.Décomposons
 en une composante
en une composante  tangente à
tangente à 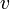 et une composante
et une composante 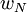 normale à
normale à 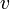 . En particulier, posons
. En particulier, posons 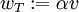 ,
, 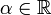 .
.L'étape précédente implique alors directement :
Il faut donc montrer que le second terme est nul, car, selon le lemme de Gauss, on devrait avoir
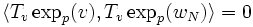 :
:
Fichier:Gauss lemma proof.pngLa courbe choisie pour prouver le lemmedéfinissons la courbe
avec
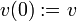 et
et 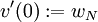 . On remarque au passage que
. On remarque au passage quePosons alors
et calculons :
et
Donc,
On va vérifier maintenant que ce produit scalaire est en fait indépendant de la variable t, et donc que, par exemple,
car, selon ce qui a été donné plus haut,
étant donné que la différentielle est une application linéaire ! Ceci prouverait alors le lemme.
- On vérifie que
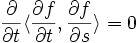 : c'est du calcul direct. En effet, on prend d'abord conscience du fait que les applications
: c'est du calcul direct. En effet, on prend d'abord conscience du fait que les applications 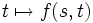 sont des géodésiques, i.e.
sont des géodésiques, i.e. 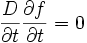 . Alors,
. Alors,
Donc, en particulier,
car on a | v | = cste.
Voir aussi
Références
Catégorie : Géométrie riemannienne
Wikimedia Foundation. 2010.

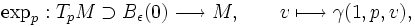
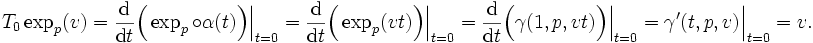

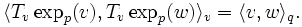

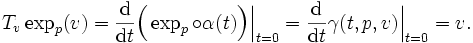
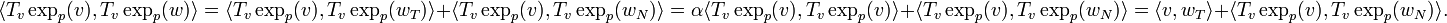
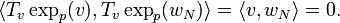
![\alpha : ]-\epsilon, \epsilon[\times [0,1] \longrightarrow T_pM,\qquad (s,t) \longmapsto t\cdot v(s),](/pictures/frwiki/56/858acd50e9bf9b6c7d9a2a92e8470eed.png)
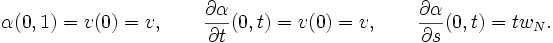
![f : ]-\epsilon, \epsilon[\times [0,1] \longrightarrow M,\qquad (s,t)\longmapsto \exp_p(t\cdot v(s)),](/pictures/frwiki/102/f9d1593414a9807b10db2904f061dc83.png)