- Lemme d'Arden
-
En théorie des automates, le lemme d'Arden est un résultat concernant les langages rationnels.
Il permet de résoudre des équations du type :
où A et B sont deux langages rationnels et X l'inconnue recherchée. Le lemme d'Arden s'utilise notamment dans la méthode des équations linéaires gauches qui permet de calculer le langage reconnu par un automate fini donné.
Sommaire
Énoncé
Soient A un langage rationnel ne contenant pas le mot vide
, et B un autre langage rationnel. 
est l'unique solution de l'équationPreuve
- Que A contienne ou pas, est solution. En effet,
Par définition,
d'où :
et ainsi
- Si A ne contient pas , alors cette solution est la seule. Supposons en effet qu'il existe deux solutions distinctes Y et Z. On peut supposer par exemple
.
Soit alors
de longueur minimale (non nécéssairement unique).Comme
et 
puisque 
, on a 
. Alors, vu que 
, 
et m = a.n avec 
.Comme
et 
puisque , on a 
d'où 
.m ayant été choisi de longueur minimale, on en déduit que
, et donc 
.Application
Le lemme d'Arden permet, par la résolution d'un système d'équation par substitution, de déterminer le langage reconnu par un automate fini.
Soit
un automate fini. On énumère les états de Q : Q = {1,...,n}. On pose alors, pour 
, Lq le langage reconnu à partir de l'état q, c'est-à-dire le langage reconnu par l'automate 
. On pose enfin 
. On écrit
où 
L'application du lemme d'Arden permet alors d'éliminer une à une les inconnues Lq des n équations de la forme précédente, et d'obtenir une expression explicite des Lq et notamment des
qui permettent de déterminer le langage reconnu par l'automate 
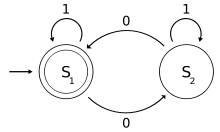
.Exemple
On écrit
et 
.Le lemme d'Arden donne
. En injectant cette expression de L2 dans l'expression précédente de L1 et en factorisant, on obtient 
et par application du lemme d'Arden,
.Liens externes
Catégories :- Théorème d'informatique
- Langage formel
Wikimedia Foundation. 2010.
