Invariance d'echelle
- Invariance d'echelle
-
Invariance d'échelle
Il y a invariance d'échelle lorsqu'aucune échelle ne caractérise le système.
Par exemple, dans un ensemble fractal, les propriétés seront les mêmes quelle que soit la distance à laquelle on se place. Une fonction g est dite invariante d'échelle s'il existe une fonction Φ telle que pour tout x et y :
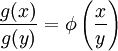
Alors, il existe une constante C et un exposant γ, tels que :
g(x) = Cxγ.
Remarque : en physique, l'invariance d'échelle n'est valable que dans un domaine de taille limité — par exemple, pour un ensemble fractal, on ne peut pas se placer à une échelle plus petite que celle des molécules, ni plus grande que la taille du système.
 Portail des mathématiques
Portail des mathématiques
Catégories : Théorie des ensembles | Fractale
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Invariance d'echelle de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Invariance D'échelle — Il y a invariance d échelle lorsqu aucune échelle ne caractérise le système. Par exemple, dans un ensemble fractal, les propriétés seront les mêmes quelle que soit la distance à laquelle on se place. Une fonction g est dite invariante d échelle s … Wikipédia en Français
Invariance d'échelle — Le processus de Wiener est invariant d échelle. Il y a invariance d échelle lorsqu aucune échelle ne caractérise le système. Par exemple, dans un ensemble fractal, les propriétés seront les mêmes quelle que soit la distance à laquelle on se place … Wikipédia en Français
Invariance — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « Invariance », sur le Wiktionnaire (dictionnaire universel) L invariance peut désigner : Physique… … Wikipédia en Français
Invariance (physique) — Symétrie (physique) En physique la notion de symétrie, appelée aussi invariance, renvoie à la possibilité de considérer un même système physique selon plusieurs points de vues distincts en termes de description mais équivalents quant aux… … Wikipédia en Français
PARTICULES ÉLÉMENTAIRES - Présentation générale — Les physiciens poursuivent l’étude de la structure de la matière dans le but de trouver plus d’unité et de simplicité dans un monde qui nous frappe par sa diversité et sa complexité apparente. N’est il pas remarquable de pouvoir ramener la… … Encyclopédie Universelle
FORME — L’histoire du concept de forme et des théories de la forme est des plus singulières. Nous vivons dans un monde constitué de formes naturelles. Celles ci sont omniprésentes dans notre environnement et dans les représentations que nous nous en… … Encyclopédie Universelle
STATISTIQUE (MÉCANIQUE) — La mécanique statistique a pour but d’expliquer les propriétés de la matière, en particulier ses propriétés thermiques, à partir des lois de la mécanique auxquelles obéissent les atomes et molécules dont elle est formée (et, plus généralement,… … Encyclopédie Universelle
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Diffusion fortement inélastique — Diffusion profondément inélastique Diagramme de la diffusion profondément inélastique d un électron sur un proton par l intermédiaire d un photon virtuel. A l issue de l interaction le proton est devenu un ensemble de particules hadroniques… … Wikipédia en Français
Diffusion profondément inélastique — Diagramme de la diffusion profondément inélastique d un électron sur un proton par l intermédiaire d un photon virtuel. A l issue de l interaction le proton est devenu un ensemble de particules hadroniques marqué ici par la lettre X. Les lettres… … Wikipédia en Français