- Inv
-
Involute
Sommaire
Domaine d'application
Fonction couramment utilisée pour le taillage des engrenages.
Définition
Involute : angle caractéristique d'une développante de cercle permettant de localiser un point M de la développante du cercle de centre O.
Cet angle QOM est formé par le rayon du cercle de base passant par le pied de la développante Q et le segment joignant le centre du cercle de base O et le point à localiser M.
Sa valeur est définie par la relation inv α = tan α - α où α représente l'angle compris entre le rayon passant par le point de tangence T de la droite roulant sans glisser sur le cercle de base et le rayon passant par le point à situer M, le rayon OM.
La relation s'établit facilement en considérant que, du fait du roulement sans glissement entre la droite et le cercle de base, l'arc de cercle QM a une longueur égale à celle du segment TM.
La localisation du point M est complétée en considérant que OM cos α = rb.
Fonction
Soit α l'angle (en radian) suivant une développante de cercle, la fonction involute vaut :
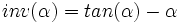
Développante de cercle
Développante de cercle : courbe caractérisant la trajectoire d'un point d'une droite roulant sans glisser sur un cercle de rayon rb appelé cercle de base. Cette courbe présente un point de rebroussement Q appelé pied de la développante. Ce point est situé sur le cercle de base.
C’est la courbe que trace la main droite déroulant une bobine de fil tenue dans la main gauche.
Voir aussi
Articles connexes
Documentation externe
Liens externes :
- Portail de la géométrie
Catégorie : Fonction remarquable
Wikimedia Foundation. 2010.
