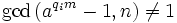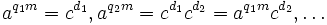Algorithme p-1 de pollard

L'algorithme p − 1 de Pollard est un algorithme de l'arithmétique modulaire pour la décomposition en produit de facteurs premiers, conçu par John Pollard en 1974. C’est un algorithme spécifique, par opposition à généraliste, car il est adapté à la factorisation de nombres entiers dont au moins un des facteurs a une forme particulière.

Sommaire 1 Friabilité 2 Principe 3 Exemple d'un cas particulier 4 Algorithme et temps d’exécution 5 Variante pour les grands nombres premiers 6 Conséquence cryptologique

Friabilité

La friabilité — en anglais smoothness — d'un nombre entier n est le fait de n'avoir que des « petits » nombres premiers comme facteurs. Généralement, on définit un seuil de friabilité, B, et un entier n est dit B-friable si tous ses diviseurs premiers sont plus petit que le seuil B. Assez naturellement, cette notion se retrouve dans plusieurs algorithmes de factorisation --- on peut considerer comme plus facile de trouver de petits facteurs.

La « bonne » notion de friabilité pour l'algorithme p − 1 considère toutes les puissances premières divisant n : l'entier n est dit B-superfriable si toutes ses diviseurs de la forme pⁱ, p premier et i entier, sont inferieurs à B. (Le terme superfriable a été inventé pour les besoins de cet article, faute de connaître l'équivalent usuel en français de l'anglais powersmooth.)

Principe

Soit n un entier divisible par un nombre premier p, avec 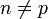. Par le petit théorème de Fermat, nous savons que

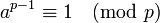pour a premier avec p. Ici (mod) désigne la congruence sur les entiers.

Cela implique que pour tout multiple M de p − 1 on a 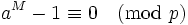car .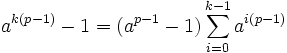

Si p − 1 est B-superfriable pour un certain seuil B, alors p − 1 divise le plus petit commun multiple des entiers de 1 à B. Donc, si on pose 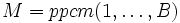, on a

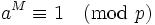pour tout a premier avec p.

Autrement dit, p divise a^M − 1 et donc le pgcd de n et a^M − 1 est supérieur ou égal à p. En revanche, il est possible que ce pgcd soit égal à n lui-même auquel cas, on n'obtient pas de facteur non trivial.

Exemple d'un cas particulier

Soit n = pqr, où p et q sont des nombres premiers distinct et r est un nombre entier, tel que p − 1 est B-friable et q − 1 n’est pas B-friable. Maintenant, pgcd(a^M − 1, n) fournit un facteur propre de n.

Notez que dans le cas où q − 1 est à B-friables, le pgcd peut produire un facteur trivial parce que q divise a^M − 1.

Notez que c’est ceci qui rend l’algorithme spécifique. Par exemple, 172189 = 421 × 409. 421 − 1 = 2²×3×5×7 et 409 − 1 = 2³×3×17. Donc, une valeur appropriée de B serait de 7 à 16. Si B était sélectionné plus petit que 7 le pgcd aurait été de 1 et si B était sélectionné plus grand que 16 le pgcd aurait été n. Bien sur, nous ne connaissons pas quelle valeur de B est appropriée, donc ceci sera un facteur dans l’algorithme.

Pour accélérer les calculs, nous savons aussi qu’en prenant le pgcd nous pouvons réduire une partie modulo l’autre, donc pgcd(a^M − 1, n) = pgcd(a^M − 1 mod n, n). Ceci peut être calculé de façon efficace en utilisant l’exponentiation modulaire et l’algorithme d'Euclide.

Algorithme et temps d’exécution

L’algorithme de base peut être écrit de la façon suivante :

Entrées : n : un entier composé

Sortie : un facteur non-trivial de n ou un échec

1. sélectionner un seuil de friabilité B
2. prendre un a aléatoirement dans 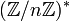(note : nous pouvons d’ore et déjà fixer a, une sélection aléatoire ici n’est pas impérative)
3. pour chaque nombre premier q ≤ B
   
   
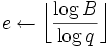
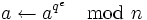
   (à la fin de cette boucle, on a a^M)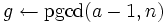
4. 
5. si 1 < g < n alors retourner g
6. si g = 1 alors sélectionner un B plus grand et aller à l’étape 2 ou retourner échec
7. si g = n alors aller à l’étape 2 ou retourner échec

Si g = 1 dans l’étape 6, ceci indique que pour tous les p − 1 il n’y en a aucun qui était B-superfriable. Si g = n dans l’étape 7, cela indique généralement que tous les facteurs étaient B-superfriables, mais dans de rares cas, il pourrait indiquer que a possède un petit ordre modulo p .

Variante pour les grands nombres premiers

Une variante de l’algorithme de base est quelquefois utilisée. Statistiquement, il existe souvent un facteur p de n tel que p − 1 = fq où f est B-friable et B < q ≤ B’, où q est un nombre premier et B’ est appelée une borne semi-friable.

Comme point de départ, ceci marcherait dans l’algorithme de base à l’étape 6 si nous avons rencontré pgcd = 1 mais que nous n’avons pas voulu augmenter B. Pour tous les nombres premiers B < q₁, …, q_L ≤ B’, nous vérifions si

pour obtenir pour un facteur non-trivial de n. Ceci est accompli rapidement, parce que si nous avons c = a^M, et d₁ = q₁ et d_i = q_i − q_{i − 1}, alors nous pouvons calculer

Le temps d’exécution de l’algorithme avec cette variante devient alors O(B’ × log B’ × log²n).

Conséquence cryptologique

L’efficacité de cet algorithme est liée à la forme des nombres premiers composant l'entier à factoriser, plus précisément à l'existence d'un facteur premier p tel que p − 1 soit B-superfriable. En conséquence, les systèmes de chiffrement à clé publique fondés sur la difficulté de la factorisation, comme par exemple RSA, imposent d'utiliser des nombres premiers n'ayant pas cette propriété pour un seuil B trop petit.

• Portail des mathématiques
• Portail de la cryptologie