Algorithme de tracé de segment fenêtré de Hadrien Flammang

L'algorithme de tracé de segment fenêtré de Hadrien Flammang permet de ne tracer d'un segment que la partie qui est visible dans une zone rectangulaire (fenêtre). Il est basé sur l'algorithme de Bresenham.

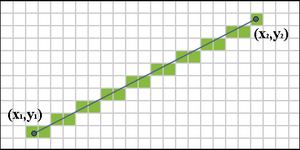
On veut tracer un segment du point de coordonnées (x₁,y₁), au point de coordonnées (x₂,y₂). Posons dx = x₂-x₁ et dy = y₂-y₁, et plaçons nous dans le cas où dx ≥ dy > 0, c'est-à-dire dans le premier octant. L'algorithme de Bresenham peut alors se résumer à trois suites X_n, Y_n et S_n qui se définissent mutuellement :

Initialisation des suites :

 X0 = x1
 Y0 = y1
 S0 = 2dY - dX

Récursion :

 Si Sn ≥ 0
 Alors
       Xn+1 = Xn + 1
       Yn+1 = Yn + 1
       Sn+1 = Sn + 2dY - 2dX
 Sinon
       Xn+1 = Xn + 1
       Yn+1 = Yn
       Sn+1 = Sn + 2dY

Rappel sur le principe de l'algorithme de Bresenham

Tracé d'un segment dans un espace discret. (0,0) est au coin bas gauche, ordonnées montantes

Il s'agit d'approcher un segment de droite défini dans un plan mathématique par une suite de pixels sur un dispositif d'affichage. Les pixels étant contraints à des coordonnées entières, et à part dans des cas triviaux, on va commettre une erreur d'arrondi. Dans le cas particulier où nous nous sommes placés (le premier octant) l'abscisse des pixels est incrémentée à chaque itération alors que l'ordonnée peut rester inchangée. Tout le problème est de déterminer quand l'ordonnée doit être incrémentée pour minimiser l'erreur avec le segment mathématique. La valeur de S_n représente l'erreur d'arrondi pour le n-ème pixel. Quand cette valeur dépasse un certain seuil c'est qu'il est temps d'incrémenter l'ordonnée. D'où le test sur S qui conditionne l'incrémentation de Y.

Le fenêtrage

Segment tracé dans son intégralité

Le problème du fenêtrage se pose quand on ne veut tracer d'un segment que la partie qui est visible dans une fenêtre. Il existe plusieurs algorithmes permettant de réaliser le fenêtrage.^[1]

Segment fenêtré : après calcul des points d'entrée et sortie, les pixels allumés ne sont pas exactement les mêmes

Pour la plupart, ils consistent à calculer le point d'entrée et de sortie du segment dans la fenêtre puis à lancer un tracé de segment classique entre ces 2 points. Cette technique a une contrainte qui peut poser problème : les pixels qui vont être "allumés" ne sont pas ceux qui l'auraient été si le segment avait été tracé dans son intégralité. Un algorithme "idéal" allumerait exactement les mêmes pixels. Ceci est réalisable de manière triviale en lançant le calcul des pixels du segment total mais en testant l'appartenance de chaque pixel à la fenêtre. Malheureusement les performances d'un tel algorithme seraient lamentables.

L'algorithme de Hadrien Flammang

L'idée est de calculer X_n, Y_n, et S_n à l'endroit où le segment entre dans la fenêtre, puis de lancer le tracer de segment avec ces valeurs initiales. De cette façon, les pixels allumés seront exactement les mêmes que si le segment avait été entièrement tracé (c'est-à-dire comme si on avait itéré n fois à partir de X₀, Y₀, et S₀).

Cherchons en un premier temps à calculer S_n, et nous verrons que X_n et Y_n viennent rapidement.

Pour comprendre comment on résout le problème, il faut remarquer qu'à chaque itération S est incrémenté de 2dY, et que s'il était positif ou nul, il est en plus décrémenté de 2dX. Donc, la plus grande valeur que peut prendre S_n est atteinte losque S_n-1 = -1. Dans ce cas, S_n = S_n-1 + 2dY = 2dY - 1, sauf peut-être à l'initialisation. Mais S₀ = 2dY - dX ≤ 2dY - 1 puisque dX ≥ 1, donc 2dY - 1 est bien la plus grande valeur possible de S.

De la même façon, la plus petite valeur de S_n est atteinte lorsque S_n-1 = 0 car alors S_n = 2dY - 2dX, et S₀ = 2dY-dX > 2dY - 2dX. Nous savons donc maintenant que S_n varie dans l'intervalle 〚 2dY - 2dX ; 2dY - 1 〛, c'est-à-dire qu'il peut prendre 2dX valeurs distinctes au maximum. Essayons donc de calculer S_n : supposons que n points aient été tracés et qu'il y ait eu x pas en Y, c'est-à-dire que S a été n fois incrémenté de 2dY et x fois décrémenté de 2dX.

On a donc : S_n = S₀ + n.2dY - x.2dX = 2dY - dX + 2.n.dY - 2.x.dX. Or, nous savons que S_n ne peut prendre que 2dX valeurs distinctes, il est donc clair qu'une seule valeur de x convient (le facteur de x étant justement 2dX). Prenons donc le cas où S_n prend sa plus grande valeur, et déduisons-en x : S_n = 2dY - dX + 2.n.dY - 2.x.dX = 2dY-1. On trouve x = ( 2.n.dY - dX + 1) div 2dX.

Sachant que d'une façon générale (A div B)*B = A - (A mod B), il vient :

                Sn = ( 2.n.dY + dX ) mod 2dX + 2dY - 2dX

Par un raisonnement similaire, on trouve Y_n = Y₀ + ( 2ndY + dX ) div 2dX + 2dY - 2dX, et trivialement X_n = X₀ + n. Il peut être utile aussi de calculer n à partir de X_n et Y_n : n = X_n - X₀, ou encore n = ( 2dX( Y_n - Y₀ ) - dX - 1 ) div 2dY + 1.

Voyons maintenant, comment, à partir de ces formules, il va être possible de calculer tous les paramètres de l'algorithme de Bresenham, au point d'entrée dans la fenêtre.

Soient x_min et x_max les limites en X de la fenêtre, et y_min et y_max les limites en Y. Nous allons énumérer les tests à effectuer pour établir la position du segment par rapport à la fenêtre, et déterminer s'il y a lieu x_d, y_d et s_d, les valeurs initiales des suites X, Y et S. (Les tests doivent être executés dans l'ordre où ils sont donnés.)

 Si x1 > xmax ou x2 < xmin
 Alors
       <le segment est entièrement en dehors de la fenêtre.> (1)

 Si y1 > ymax ou y2 < ymin
 Alors
       <le segment est entièrement en dehors de la fenêtre.> (2)

 Si (x1 < xmin) et ((y1 + ( 2(xmin - x1).dY + dX) div 2dX ≥ ymin) ou (y1 ≥ ymin))
 Alors
       Si (y1 + ( 2( xmin - x1 )dY + dX ) div 2dX) ≥ ymax
       Alors
             <le segment est entièrement en dehors de la fenêtre.> (3)
       Sinon
             <le segment entre dans la fenêtre par la gauche.>  (4)
             n  ← xmin-x1
             xd ← xmin
             yd ← y1 + ( 2ndY + dX ) div 2dX
             sd ← ( 2ndY + dX ) mod 2dX + 2dY - 2dX

 Si y1 < ymin
 Alors
       Si x1 + ( 2dX( ymin - y1 ) - dX - 1 ) div 2dY + 1  >  xmax
       Alors
             <le segment est entièrement en dehors de la fenêtre.> (5)
       Sinon
             <le segment entre dans la fenêtre par le bas.>  (6)
             n  ← ( 2dX( ymin - y1 ) - dX - 1 ) div 2dY + 1
             xd ← x1 + n
             yd ← ymin
             sd ← ( 2ndY + dX ) mod 2dX + 2dY - 2dX
 Sinon
       <le premier point du segment est dans la fenêtre.>   (7)
       xd ← x1
       yd ← y1
       sd ← 2dY - dX

Détermination de x_f, l'abscisse d dernier point à tracer :

   Si y2 > ymax et ( x2 ≤ xmax ou (y1 + 2dY(xmax - x1) + dX) div 2dX > ymax )
   Alors
         n ← ( 2dX( ymax - y1 ) - dX - 1 ) div 2dY
         xf ← x1 + n
   Sinon
         Si x2 > xmax
         Alors
               xf ← xmax
         Sinon
               xf ← x2

Il ne reste plus qu'à tracer le segment du point (x_d,y_d) jusquà ce qu'il atteigne le point d'abscisse x_f, avec l'erreur initiale S :

   x = xd
   y = yd
   s = sd
   Tant que ( x ≤ xf )
       Plot( x,y )
       x ← x + 1
       Si s ≥ 0
       Alors
             y ← y + 1
             s ← s + 2dY - 2dX
       Sinon
             s ← s + 2dY

• Portail de l’informatique
• Portail de la géométrie