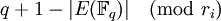Algorithme de schoof

Algorithme de Schoof

L'algorithme de Schoof est un algorithme décrit pour la première fois en 1985 par R. Schoof, permettant de déterminer le nombre de points sur une courbe elliptique, particulièrement pour la cryptographie sur les courbes elliptiques.

Principe

Le théorème de Hasse sur les courbes elliptiques fournit l'approximation :

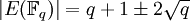$|E(\mathbb{F}_q)| = q + 1 \pm 2 \sqrt{q}$ ,

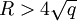alors pour trouver le nombre exact de points, il est suffisant de trouver ce nombre modulo $R > 4 \sqrt{q}$ .

L'algorithme de Schoof calcule

$q+1 - |E(\mathbb{F}_q)| \pmod{r_i}$

pour plusieurs petits nombres premiers $r i$ , où 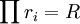$\prod r_i = R$ . Le résultat final est obtenu par combinaison via le théorème des restes chinois.

Analyse

La complexité de l'algorithme original est $(log q) 8$ et a été améliorée à $O ((log q) 6)$ . C'est une complexité pratique pour un ordinateur personnel, avec $q < 256$ .

L'algorithme a été étendu par Noam Elkies et A. O. L. Atkin pour donner l'algorithme de Schoof-Elkies-Atkin, qui a une meilleure complexité asymptotique, de $O ((log q) 5)$ .

Référence

R. Schoof, Elliptic curves over finite fields and the computation of square roots mod p, Mathematics of Computation, Volume 44, 1985.

Portail des mathématiques
Portail de la cryptologie

Ce document provient de « Algorithme de Schoof ».

Catégorie : Algorithme de cryptographie

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Algorithme de schoof de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

Algorithme De Schoof — L algorithme de Schoof est un algorithme décrit pour la première fois en 1985 par R. Schoof, permettant de déterminer le nombre de points sur une courbe elliptique, particulièrement pour la cryptographie sur les courbes elliptiques. Principe Le… … Wikipédia en Français
Algorithme de Schoof — L algorithme de Schoof est un algorithme décrit pour la première fois en 1985 par René Schoof, permettant de déterminer le nombre de points sur une courbe elliptique, particulièrement pour la cryptographie sur les courbes elliptiques. Principe Le … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français
Noam Elkies — Noam David Elkies Noam Elkies en 2007 à Oberwolfach Naissance 25 août 1966 New York (États Unis) Nationalité Américaine Isr … Wikipédia en Français
Cryptographie Sur Les Courbes Elliptiques — En cryptographie, les courbes elliptiques, des objets mathématiques, peuvent être utilisées pour des opérations asymétriques comme des échanges de clés sur un canal non sécurisé ou un chiffrement asymétrique, on parle alors de cryptographie sur… … Wikipédia en Français
Cryptographie par courbe elliptique — Cryptographie sur les courbes elliptiques En cryptographie, les courbes elliptiques, des objets mathématiques, peuvent être utilisées pour des opérations asymétriques comme des échanges de clés sur un canal non sécurisé ou un chiffrement… … Wikipédia en Français
Cryptographie sur les courbes elliptiques — En cryptographie, les courbes elliptiques, des objets mathématiques, peuvent être utilisées pour des opérations asymétriques comme des échanges de clés sur un canal non sécurisé ou un chiffrement asymétrique, on parle alors de cryptographie sur… … Wikipédia en Français
Cryptologie sur les courbes elliptiques — Cryptographie sur les courbes elliptiques En cryptographie, les courbes elliptiques, des objets mathématiques, peuvent être utilisées pour des opérations asymétriques comme des échanges de clés sur un canal non sécurisé ou un chiffrement… … Wikipédia en Français
Théorème de Hasse — En mathématiques, le théorème de Hasse sur les courbes elliptiques limite le nombre de points d une courbe elliptique sur un corps fini, au dessus et en dessous. Si N est le nombre de points d une courbe elliptique E sur un corps fini à q… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Algorithme de schoof