Algorithme de Prim

Pour les articles homonymes, voir Prim.

Arbre couvrant de poids minimum

L'algorithme de Prim est un algorithme glouton qui permet de trouver un arbre couvrant minimal dans un graphe connexe valué et non-orienté. En d'autres termes, cet algorithme trouve un sous-ensemble d'arêtes formant un arbre sur l'ensemble des sommets du graphe initial, et tel que la somme des poids de ces arêtes soit minimale. Si le graphe n'est pas connexe, alors l'algorithme ne déterminera l'arbre couvrant minimal que d'une composante connexe du graphe. Il a été conçu en 1957 par Robert Prim.

Principe

L'algorithme consiste à choisir arbitrairement un sommet et à faire croître un arbre à partir de ce sommet. Chaque augmentation se fait de la manière la plus économique possible.

Algorithme

Procédure PRIM
 Paramètres locaux : entier s, graphe G
 Paramètres globaux : graphe T
 Variables : 
  entier i, m, y
  réel : v
  ensemble : M
  TvectNent : pp
  TvectNReel : d 
Début 
1  T ← graphe_vide
2  M ← ensemble_vide
3  Pour i ← 0 jusqu'à N Faire
4    d[i] ←coût(s, i, G)
5    pp[i] ← s 
6    M ← Ajouter (i,M)
7  Fin pour
8  M ← Supprimer (s,M)
9  Tant que M <> Ensemble_vide Faire
10   m ← Choisir (M,d)
11   M ← Supprimer (m,M)
12   z ← pp[m]
13   v ← coût (m,z,G)
14   T ← Ajout arête <m,z> de coût v à T
15   Pour i ← 1 jusqu'à d° m dans G Faire
16     y ← i ième_succ_de m dans G
17     Si y  M et (cout(m,y,G) < d[y]) alors
18       d[y] ← coût(m,y,G)
19       pp[y] ← m
20     Fin Si
21   Fin Pour
22 Fin Tant que
Fin algo

(Attention, le principe suivant diffère de l'implémentation proposée).

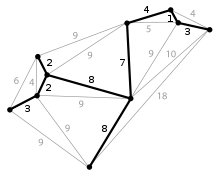
L'étape d'initialisation consiste à choisir un sommet quelconque du graphe initial. Au bout de la première étape, on se retrouve ainsi avec un arbre contenant 1 sommet et 0 arête. Ensuite, on construit récursivement l'arbre minimal de la façon suivante : à l'étape n, ayant déjà construit un arbre contenant n sommets et n-1 arêtes, on établit la liste de toutes les arêtes reliant un sommet de l'arbre à un sommet qui n'est pas sur l'arbre. On choisit alors une arête de poids minimal, que l'on rajoute à l'arbre ; l'arbre contient à présent n+1 sommets et n arêtes. L'algorithme se termine lorsque tous les sommets du graphe sont contenus dans l'arbre.

La complexité de l'algorithme dépend fortement de la manière dont est implémenté le choix de l'arête/sommet à ajouter dans l'ensemble à chaque étape. Avec une représentation naïve, on obtient une complexité en O(A * S) avec A le nombre d'arêtes et S le nombre de sommets. Si l'on utilise un tas min binaire, la complexité devient alors O(A * lgS). En utilisant un tas de Fibonacci, on peut encore descendre à O(A + S * lgS).

Références

J.-F. Hêche, ROSO-EPFL, Cours SC de recherche opérationnelle : Quelques problèmes classiques en théorie des graphes

T. H. Cormen, C. E. Leiserson, R. L. Rivest, C. Stein : Introduction à l'algorithmique

Liens internes

• Algorithme de Kruskal

• Portail de l’algorithmique
• Portail des mathématiques