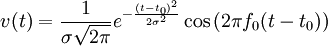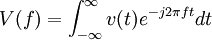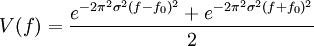Impulsion de gabor

Impulsion de gabor

Impulsion de Gabor

L'impulsion de Gabor est plus connue sous le nom de gaussienne modulée. C'est une fonction mathématique utilisée comme signal d'excitation dans les simulateurs d'électromagnétisme. Elle présente l'avantage d'être infiniment dérivable, et elle hérite de la propriété fondamentale de la gaussienne : son invariance de forme par la transformation de Fourier.

Expression générale de l'impulsion de Gabor

La gaussienne modulée est un simple produit entre une gaussienne et une sinusoïde :

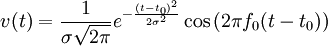
v(t)=\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(t-t_0)^2}{2\sigma^2}}\cos \left(2 \pi f_0(t-t_0) \right)

où :

  • t0 est un retard permettant d'avoir le début de la gaussienne en temps positif
  • f0 est la fréquence centrale de la gaussienne duale obtenue après transformation de Fourier (dans un simulateur électromagnétique par exemple, on la choisirait de manière à ne pas exciter les modes en dessous d'une certaine fréquence)
  • σ est l'écart-type de la gaussienne (il va donc influer sur la fréquence haute dans le domaine fréquentiel)

Domaine fréquentiel

On s'intéresse à la transformée de Fourier de l'impulsion de Gabor.

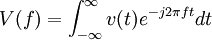
V(f)=\int_{- \infty}^\infty v(t) e^{-j2\pi f t} dt

Sachant que :

  • la transformée de Fourier d'une gaussienne est également une gaussienne, d'écart-type inverse
  • la transformée de Fourier d'une sinusoïde est une impulsion de Dirac

les propriétés du produit de convolution permettent de conclure après un petit calcul que :

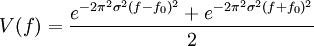
V(f)=\frac{e^{-2\pi^2\sigma^2(f-f_0)^2}+e^{-2\pi^2\sigma^2(f+f_0)^2}}{2}
  • Portail de la physique Portail de la physique
  • Portail de l’électricité et de l’électronique Portail de l’électricité et de l’électronique
Ce document provient de « Impulsion de Gabor ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Impulsion de gabor de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

  • Impulsion De Gabor — L impulsion de Gabor est plus connue sous le nom de gaussienne modulée. C est une fonction mathématique utilisée comme signal d excitation dans les simulateurs d électromagnétisme. Elle présente l avantage d être infiniment dérivable, et elle… …   Wikipédia en Français

  • Impulsion de Gabor — L impulsion de Gabor, du nom du physicien hongrois Dennis Gabor, est plus connue sous le nom de gaussienne modulée. C est une fonction mathématique utilisée comme signal d excitation dans les simulateurs d électromagnétisme. Elle présente l… …   Wikipédia en Français

  • Budapest — Héraldique …   Wikipédia en Français

  • Claustrophobie quantique — Principe d incertitude Vues spatiale (position) et fréquentielle (impulsion) de (a) une onde, (b) un paquet d onde et (c) un corpuscule.L onde étant de fréquence pure, son impulsion est définie mais elle n est pas localisée dans l espace.… …   Wikipédia en Français

  • Inégalité d'Heisenberg — Principe d incertitude Vues spatiale (position) et fréquentielle (impulsion) de (a) une onde, (b) un paquet d onde et (c) un corpuscule.L onde étant de fréquence pure, son impulsion est définie mais elle n est pas localisée dans l espace.… …   Wikipédia en Français

  • Inégalité de Heisenberg — Principe d incertitude Vues spatiale (position) et fréquentielle (impulsion) de (a) une onde, (b) un paquet d onde et (c) un corpuscule.L onde étant de fréquence pure, son impulsion est définie mais elle n est pas localisée dans l espace.… …   Wikipédia en Français

  • Inégalités de Heisenberg — Principe d incertitude Vues spatiale (position) et fréquentielle (impulsion) de (a) une onde, (b) un paquet d onde et (c) un corpuscule.L onde étant de fréquence pure, son impulsion est définie mais elle n est pas localisée dans l espace.… …   Wikipédia en Français

  • Principe d'incertitude — Vues spatiale (position) et fréquentielle (impulsion) de (a) une onde, (b) un paquet d onde et (c) un corpuscule. L onde étant de fréquence pure, son impulsion est définie mais elle n est pas localisée dans l espace. Inversement, le corpuscule… …   Wikipédia en Français

  • Principe d'incertitude d'Heisenberg — Principe d incertitude Vues spatiale (position) et fréquentielle (impulsion) de (a) une onde, (b) un paquet d onde et (c) un corpuscule.L onde étant de fréquence pure, son impulsion est définie mais elle n est pas localisée dans l espace.… …   Wikipédia en Français

  • Principe d'incertitude de Heisenberg — Principe d incertitude Vues spatiale (position) et fréquentielle (impulsion) de (a) une onde, (b) un paquet d onde et (c) un corpuscule.L onde étant de fréquence pure, son impulsion est définie mais elle n est pas localisée dans l espace.… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”