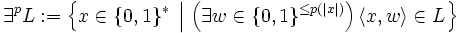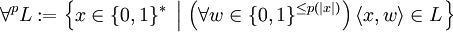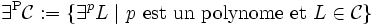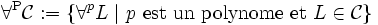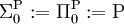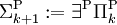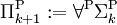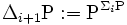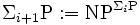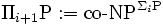Hiérarchie Polynomiale

Hiérarchie polynomiale

La hiérarchie polynômiale est une hiérarchie de classes de complexité de problèmes, qui étend la notion de classes P, NP, co-NP.

Définition

Quanteurs

On peut définir la hiérarchie à l'aide des quanteurs pour-tout et il-existe. Soit $p$ un polynôme, et $L$ un langage.

$\exists^p L := \left\{ x \in \{0,1\}^* \ \left| \ \left( \exists w \in \{0,1\}^{\leq p(|x|)} \right) \langle x,w \rangle \in L \right. \right\}$

c'est-à-dire que 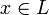$x\in L$ quand il existe un mot $w$ relativement petit (polynômialement) qui peut en témoigner. De la même façon on définit

$\forall^p L := \left\{ x \in \{0,1\}^* \ \left| \ \left( \forall w \in \{0,1\}^{\leq p(|x|)} \right) \langle x,w \rangle \in L \right. \right\}$

On étend ces définition aux classes de langages : ainsi

$\exists^{\rm P} \mathcal{C} := \left\{ \exists^p L \ | \ p \mbox{ est un polynome et } L \in \mathcal{C} \right\}$

$\forall^{\rm P} \mathcal{C} := \left\{ \forall^p L \ | \ p \mbox{ est un polynome et } L \in \mathcal{C} \right\}$

Alors, on peut enfin donner les définitions des classes de la hiérarchie polynômiale par

$\Sigma_0^{\rm P} := \Pi_0^{\rm P} := {\rm P}$

$\Sigma_{k+1}^{\rm P} := \exists^{\rm P} \Pi_k^{\rm P}$

$\Pi_{k+1}^{\rm P} := \forall^{\rm P} \Sigma_k^{\rm P}$

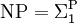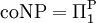En particulier, ${\rm NP} = \Sigma_1^{\rm P}$ et ${\rm coNP} = \Pi_1^{\rm P}$ .

Oracles

La hiérarchie polynômiale est également définissable à l'aide de machine de Turing avec oracle. $A B$ dénote la classe des machines de complexité $P$ augmentées d'un oracle de complexité $B$ .

On pose

Δ 0 P = Σ 0 P = Π 0 P = P

Puis pour tout i≥0 :

$\Delta_{i+1}\mbox{P} := \mbox{P}^{\Sigma_i\rm{P}}$

$\Sigma_{i+1}\mbox{P} := \mbox{NP}^{\Sigma_i\rm{P}}$

$\Pi_{i+1}\mbox{P} := \mbox{co-NP}^{\Sigma_i\rm{P}}$

Ce document provient de « Hi%C3%A9rarchie polynomiale ».

Catégorie : Logique mathématique

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Hiérarchie Polynomiale de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

Hierarchie polynomiale — Hiérarchie polynomiale La hiérarchie polynômiale est une hiérarchie de classes de complexité de problèmes, qui étend la notion de classes P, NP, co NP. Définition Quanteurs On peut définir la hiérarchie à l aide des quanteurs pour tout et il… … Wikipédia en Français
Hiérarchie polynomiale — Représentation graphique de la hiérarchie polynomiale. Les flèches indiquent l inclusion. En théorie de la complexité, la hiérarchie polynomiale est une hiérarchie de classes de complexité qui étend la notion de classes P, NP, co NP. Définition… … Wikipédia en Français
Polynomiale Hierarchie — Dieser Artikel oder Abschnitt bedarf einer Überarbeitung. Näheres ist auf der Diskussionsseite angegeben. Hilf mit, ihn zu verbessern, und entferne anschließend diese Markierung. Die Polynomialzeithierarchie (PH, auch: polynomielle Hierarchie)… … Deutsch Wikipedia
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Oracle (machine de Turing) — Pour les articles homonymes, voir Oracle et Turing (homonymie). En théorie de la complexité ou de la calculabilité, les machines de Turing avec oracle sont une variante des machines de Turing. On peut les voir comme une machine de Turing… … Wikipédia en Français
Oracle (machine de turing) — Pour les articles homonymes, voir Oracle et Turing (homonymie). En théorie de la complexité ou de la calculabilité, les machines de Turing avec oracle sont une variante des machines de Turing. On peut les voir comme une machine de Turing… … Wikipédia en Français
Sharp-P — #P, prononcé sharp P (ou dièse P ), est une classe de complexité. Contrairement à la plupart des autres classes de complexité, ce n est pas une classe de problèmes de décision mais une classe de fonctions calculables. Il s agit de compter le… … Wikipédia en Français
Sharp-p — #P, prononcé sharp P (ou dièse P ), est une classe de complexité. Contrairement à la plupart des autres classes de complexité, ce n est pas une classe de problèmes de décision mais une classe de fonctions calculables. Il s agit de compter le… … Wikipédia en Français
Théorie des équations (histoire des sciences) — Pour les articles homonymes, voir Théorie des équations. Évariste Galois offre une condition nécessaire et suffisante à la résolution d une équation polynomiale par l’algèbre. Il … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Hiérarchie Polynomiale