Hartree-Fock

Hartree-Fock: Méthode de Hartree-Fock

Méthodes numériques
pour le calcul de la structure électronique

Hartree-Fock

Théorie de la perturbation de Møller-Plesset

Interaction de configuration

Méthode du cluster couplé

Champ multi-configurationnel auto-cohérent

Théorie de la fonctionnelle de la densité

La méthode de Hartree-Fock est une méthode de résolution approchée de l'équation de Schrödinger d'un système quantique à N fermions utilisant le principe variationnel dans laquelle la fonction d'onde approchée est écrite sous la forme d'un déterminant de Slater :
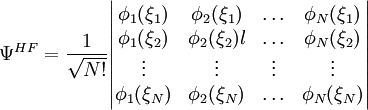
$\Psi^{HF} = {1\over\sqrt {N!}}\begin{vmatrix} \phi_1 (\xi_1) & \phi_2 (\xi_1) &\ldots &\phi_N (\xi_1) \\ \phi_1 (\xi_2) & \phi_2 (\xi_2) l &\ldots &\phi_N (\xi_2) \\ \vdots &\vdots &\vdots &\vdots\\ \phi_1 (\xi_N) & \phi_2 (\xi_N) &\ldots &\phi_N (\xi_N) \\ \end{vmatrix}$
Les spinorbitales $Φ i (ξ i)$ sont les solutions d'un système d'équations différentielles couplées appelées équations de Hartree-Fock :
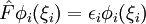
$\hat F \phi_i (\xi_i) = \epsilon_i \phi_i (\xi_i)$
où 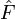$\hat F$ est l'opérateur de Fock. Dans le cas des atomes et des molécules, l'opérateur de Fock a pour expression :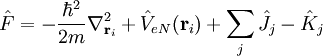
$\hat F = -\frac{\hbar^2}{2m}\nabla^2_{\mathbf r_i} + \hat V_{eN}(\mathbf r_i) + \sum\limits_j \hat J_j - \hat K_j$
L'opérateur 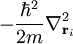$-\frac{\hbar^2}{2m}\nabla^2_{\mathbf r_i}$ correspond à l'énergie cinétique de l'électron i. L'opérateur 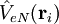$\hat V_{eN}(\mathbf r_i)$ décrit le potentiel électrostatique entre cet électron et le(s) noyau(x). L'opérateur 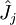$\hat J_j$ ou opérateur coulombien représente le potentiel moyen créé par les autres électrons et 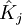$\hat K_j$ , l'opérateur d'échange, la correction à ce potentiel due à l'antisymétrie.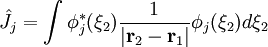
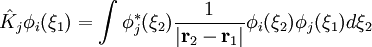
$\hat J_j = \int\phi_j^*(\xi_2)\frac{1}{\vert \mathbf r_2 - \mathbf r_1\vert} \phi_j(\xi_2)d\xi_2$ $\hat K_j\phi_i(\xi_1) = \int\phi_j^*(\xi_2)\frac{1}{\vert \mathbf r_2 - \mathbf r_1\vert} \phi_i(\xi_2)\phi_j(\xi_1)d\xi_2$
La méthode de Hartree-Fock est une approximation de champ moyen à particules indépendantes. L'opérateur de Fock dépend explicitement de ses solutions. La méthode de résolution la plus utilisée est la méthode du champ auto cohérent. Il s'agit d'une méthode itérative où l'opérateur de Fock est mis à jour à chaque itération avec les spinorbitales calculées à l'itération précédente. La calcul est arrêté lorsqu'une convergence satisfaisante (sur l'énergie, la fonction d'onde, .. etc.) est obtenue.

Le théorème de Koopmans donne aux valeurs propres $ε i$ de l'opérateur de Fock le sens physique d'opposé du potentiel d'ionisation
$P i = - ε i$
Les fonctions d'onde Hartree-Fock satisfont le théorème d'Hellmann-Feynman et le théorème du viriel.

Voir aussi les applications de ce type de méthodes en physique nucléaire.

Portail de la physique

Portail de la chimie

Ce document provient de « M%C3%A9thode de Hartree-Fock ».

Catégories : Chimie quantique | Mécanique quantique | Physique quantique

Contenu soumis à la licence CC-BY-SA. Source : Article Hartree-Fock de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

Hartree-Fock — In computational physics and computational chemistry, the Hartree Fock (HF) method is an approximate method for the determination of the ground state wavefunction and ground state energy of a quantum many body system.The Hartree Fock method… … Wikipedia
Hartree-Fock — Unter Hartree Fock Rechnung versteht man eine Methode der Theoretischen Physik, mit der man hauptsächlich Probleme der Theoretischen Chemie löst. Sie ermöglicht es, Orbitalenergien und Wellenfunktionen von quantenmechanischen Vielteilchensystemen … Deutsch Wikipedia
Hartree-Fock — La aproximación de Hartree Fock es el equivalente, en química computacional, a la aproximación de orbitales moleculares, de enorme utilidad conceptual para los químicos. Este esquema de cálculo, también llamado de campo autoconsistente, es un… … Enciclopedia Universal
Hartree-Fock-Methode — Unter Hartree Fock Rechnung versteht man eine Methode der Theoretischen Physik, mit der man hauptsächlich Probleme der Theoretischen Chemie löst. Sie ermöglicht es, Orbitalenergien und Wellenfunktionen von quantenmechanischen Vielteilchensystemen … Deutsch Wikipedia
Hartree-Fock-Methode — Har|t|ree Fọck Me|tho|de, Har|t|ree Fọck Root|haan Me|tho|de [ hɑ:trɪ ; nach D. R. Hartree, dem russ. Physiker V. A. Fock (auch W. A. Fok; 1898–1974) u. dem niederl. amer. Physikochemiker C. C. J. Roothaan (*1918)]: eine quantenchem. SCF… … Universal-Lexikon
Hartree-Fock equation — Hartrio ir Foko lygtis statusas T sritis fizika atitikmenys: angl. Hartree Fock equation vok. Hartree Fock Gleichung, f rus. уравнение Хартри Фока, n pranc. équation de Hartree Fock, f … Fizikos terminų žodynas
Hartree-Fock-Gleichung — Hartrio ir Foko lygtis statusas T sritis fizika atitikmenys: angl. Hartree Fock equation vok. Hartree Fock Gleichung, f rus. уравнение Хартри Фока, n pranc. équation de Hartree Fock, f … Fizikos terminų žodynas
Hartree-Fock method — Hartrio ir Foko metodas statusas T sritis fizika atitikmenys: angl. Hartree Fock method vok. Hartree Fock Methode, f rus. метод Хартри Фока, m pranc. méthode de Hartree Fock, f … Fizikos terminų žodynas
Hartree-Fock-Methode — Hartrio ir Foko metodas statusas T sritis fizika atitikmenys: angl. Hartree Fock method vok. Hartree Fock Methode, f rus. метод Хартри Фока, m pranc. méthode de Hartree Fock, f … Fizikos terminų žodynas
Hartree-Fock-Roothaan-Methode — Har|t|ree Fọck Me|tho|de, Har|t|ree Fọck Root|haan Me|tho|de [ hɑ:trɪ ; nach D. R. Hartree, dem russ. Physiker V. A. Fock (auch W. A. Fok; 1898–1974) u. dem niederl. amer. Physikochemiker C. C. J. Roothaan (*1918)]: eine quantenchem. SCF… … Universal-Lexikon

Dictionnaires et Encyclopédies sur 'Academic'

Hartree-Fock

Méthode de Hartree-Fock

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Hartree-Fock

Méthode de Hartree-Fock

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link