Géométrie sphérique

Géométrie sphérique
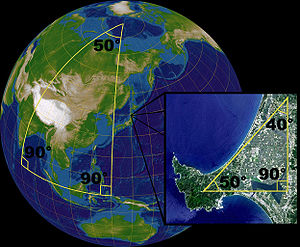Sur une sphère, la somme des angles intérieurs d'un triangle n'est pas égale à 180°. Une sphère ne relève pas d'un espace euclidien mais localement et par approximation les lois de la géométrie euclidienne peuvent s'appliquer. Par exemple dans un petit triangle délimitant une portion de la surface de la terre, la somme des angles est proche de 180°. D'autre part, une sphère peut-être décomposée en une collection de cartes à deux dimensions constituant ainsi une variété géométrique.

La géométrie sphérique est une branche de la géométrie qui s'intéresse à la surface bidimensionnelle d'une sphère. Ceci est un exemple de géométrie non euclidienne.

En géométrie plane, les concepts de base sont des points et des lignes. Sur la sphère, les points sont définis dans un sens commun. Par contre, les équivalences des lignes ne sont pas définies dans le sens commun, comme une ligne droite, mais plutôt comme le chemin le plus court entre les points, ce qui est appelé une géodésique. Sur la sphère, les géodésiques sont les grands cercles, donc les autres concepts géométriques sont définis comme dans un plan, mais avec des lignes qui remplacent les grands cercles.

Les angles de géométrie sphérique sont définis entre les grands cercles, résultant d'une trigonométrie sphérique qui diffère de la trigonométrie ordinaire sous bien des aspects. Par exemple, la somme des angles d'un triangle, en géométrie sphérique, excède 180°. C’est cet excès angulaire qui donne le signe positif de la courbure de l’espace dans cette géométrie.

La géométrie sphérique est le modèle le plus simple de géométrie elliptique (en), dans laquelle une droite n’a pas de parallèles passant par un point donné, et où l’espace présente en tout point et dans toutes les directions une courbure positive. La géométrie elliptique est dérivée de la géométrie sphérique, topologiquement équivalente, mais n’impose pas que cette courbure soit constante, juste qu'elle reste strictement positive (on peut se la représenter comme la géométrie locale tangente à la surface d’un ellipsoïde et non d’une sphère).

La géométrie sphérique a des applications pratiques importantes en navigation, en astronomie et en tectonique des plaques.

Articles connexes


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Géométrie sphérique de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

  • Geometrie spherique — Géométrie sphérique Sur une sphère, la somme des angles n est pas égale à 180°. Une sphère ne relève pas d un espace euclidien mais localement et par approximation les lois de la géométrie euclidienne peuvent s appliquer. Par exemple dans un… …   Wikipédia en Français

  • Géométrie Sphérique — Sur une sphère, la somme des angles n est pas égale à 180°. Une sphère ne relève pas d un espace euclidien mais localement et par approximation les lois de la géométrie euclidienne peuvent s appliquer. Par exemple dans un petit triangle… …   Wikipédia en Français

  • Geometrie — Géométrie La géométrie est la partie des mathématiques qui étudie les figures de l espace de dimension 3 (géométrie euclidienne) et, depuis le XVIIIe siècle, aux figures de d autres types d espaces (géométrie projective, géométrie non… …   Wikipédia en Français

  • Géometrie — Géométrie La géométrie est la partie des mathématiques qui étudie les figures de l espace de dimension 3 (géométrie euclidienne) et, depuis le XVIIIe siècle, aux figures de d autres types d espaces (géométrie projective, géométrie non… …   Wikipédia en Français

  • Géométrie différentielle des surfaces — En mathématiques, la géométrie différentielle des surfaces est la branche de la géométrie différentielle qui traite des surfaces (les objets géométriques de l espace usuel E3, ou leur généralisation que sont les variétés de dimension 2), munies… …   Wikipédia en Français

  • Géométrie non euclidienne — On appelle géométrie non euclidienne une théorie géométrique ayant recours à tous les axiomes et postulats posés par Euclide dans les Éléments, sauf le postulat des parallèles. La droite d est la seule droite passant par le point M et parallèle à …   Wikipédia en Français

  • Géométrie — Traditionnellement, la géométrie est la partie des mathématiques qui étudie les figures du plan et de l espace (géométrie euclidienne). Depuis la fin du XVIIIe siècle, la géométrie étudie également les figures appartenant à d autres types d… …   Wikipédia en Français

  • Sphèrique — Sphère Pour les articles homonymes, voir Sphère (homonymie). Une sphère dans un espace euclidien En géométrie euclidienne, une sphère es …   Wikipédia en Français

  • Sphérique — Sphère Pour les articles homonymes, voir Sphère (homonymie). Une sphère dans un espace euclidien En géométrie euclidienne, une sphère es …   Wikipédia en Français

  • GÉOMÉTRIE — La géométrie est communément définie comme la science des figures de l’espace. Cette définition un peu incertaine risque de conduire à inclure dans la géométrie des questions qui ne sont géométriques que dans leur langage, mais relèvent en fait… …   Encyclopédie Universelle

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”