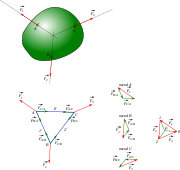
Funiculaire et dynamique

La méthode du dynamique et du funiculaire est une méthode graphique de résolution des problèmes de statique (statique graphique). Elle consiste à tracer deux diagrammes :

• le dynamique ou polygone des forces : les vecteurs force sont représentés avec une échelle donnée (par exemple 1 cm = 100 N) et mis bout à bout ; à l'équilibre, ils forment un polygone fermé, ce qui traduit le fait que la somme des forces est nulle ;
• le polygone funiculaire, ou funiculaire : sur le dessin représentant le système, on trace des segments de droite limités par les lignes d'action des forces, et à l'équilibre, on a un polygone fermé ; ceci traduit le fait que la somme des moments des forces par rapport à un point est nul (théorème de Varignon).

Le dynamique et le funiculaire sont donc une illustration graphique du principe fondamental de la statique.

Principe de la méthode

Exemple de construction d'un dynamique et d'un funiculaire (deux tracés à partir de deux points différents)

Considérons un problème de statique résolu (toutes les forces sont connues). La première étape consiste à tracer le dynamique, c'est-à-dire à dessiner à une échelle donnée les n forces mises bout à bout. On a donc un polygone fermé — bien que cela ne soit pas une nécessité, on prend les forces en progressant dans un sens, par exemple de gauche à droite, ce qui permet d'éviter que le funiculaire soit un polygone croisé. On numérote les sommets du dynamique, de 0 à n-1, dans le sens des flèches des vecteurs.

Nous considérons ci-contre un exemple avec trois forces 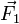, 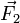et .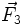

Puis, on écrit un tableau de deux lignes :

• la première ligne contient les noms des forces dans l'ordre donné par le sens des flèches ;
• la deuxième ligne indique les sommets que relient chaque force : 0 → 1, 1 → 2, …, n-1 → 0.

Forces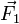
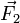
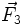
Sommets	0 → 1	1 → 2	2 → 0

On prend un point quelconque ; par convention, on le prend hors de ce polygone, à droite ou à gauche du polygone. Pour que le tracé du funiculaire soit précis et compact, il faut le prendre suffisamment loin du polygone, et sur une ligne horizontale passant à peu près au centre du polygone ; cela permet d'avoir des droites polaires (voir plus loin) peu inclinées. Ce point est appelé pôle et habituellement noté P, ou S lorsque la lettre P est déjà utilisée.

Ensuite, on relie le pôle aux sommets ; les segments de droite ainsi formés, les droites polaires, portent le nom des sommets auquel ils sont attachés.

Puis on trace le polygone funiculaire : sur le dessin du système, on prend un point arbitraire O₁ quelconque de la ligne d'action de la première force du tableau (celle reliant le sommet 0 au sommet 1 du dynamique), et on trace un segment de droite parallèle au segment 1 du dynamique que l'on arrête sur la ligne d'action de la deuxième force. Ce segment est appelé 1' (1 est le sommet du dynamique commun aux forces dont les lignes d'actions reliées par 1'), et le point d'arrêt est appelé O₂. On part de O₂ et l'on construit 2', le segment parallèle au segment 2 du dynamique et s'arrêtant sur la ligne d'action de la troisième force du tableau (2 est le sommet du dynamique commun aux forces dont les lignes d'actions reliées par 2'). Et ainsi de suite.

On obtient ainsi un polygone fermé.

Explication

Le funiculaire est en fait un treillis dont les nœuds sont sur les droites d'action des forces.

Pour qu'un solide soit en équilibre, il faut

1. Que la somme des forces soit nulle, et
2. Que la somme des moments de forces par rapport à un point quelconque soit nulle.

Ce qui importe pour le moment, c'est la hauteur du point considéré à la droite portant la force, dite ligne d'action de la force ; c'est la longueur du segment perpendiculaire à la ligne d'action passant par le point. Dans le cadre de la statique, on peut donc placer le point d'application de la force n'importe où sur cette droite d'action (ceci devient faux lorsque l'on considère les déformations ou les notions d'équilibre stable ou instable).

Le funiculaire consiste à remplacer l'objet étudié par un treillis — une structure composée de poutres articulées (liaisons pivot) — qui est en équilibre sous l'action des mêmes forces. Les segments joignant le pôle aux angles du dynamique sont les forces qui s'exercent dans ces poutres (traction ou compression).

Utilisation pour la résolution de problèmes

L'intérêt de cette construction est de pouvoir déterminer des forces inconnues et/ou des lignes d'action inconnues. Dans ce cas-là, le funiculaire est incomplet, le segment permettant de fermer le funiculaire — et donc de résoudre le problème — est appelé ligne de fermeture.

Dans l'analyse d'un problème, on peut souvent déterminer la direction d'une force inconnue, en fonction de la nature de la liaison avec son environnement ; par exemple, dans le cas d'un appui ponctuel sur un plan sans frottement, la force est perpendiculaire au plan. Si l'on ne connaît ni l'intensité ni la direction d'une force, il peut être intéressant de tracer le funiculaire à partir du point d'application de cette force, puisque c'est le seul point de la ligne d'action connu.

Lorsqu'un objet n'est pas en équilibre, la méthode permet de déterminer la résultante des forces s'exerçant sur l'objet (puisque c'est l'opposé de la force unique qui mettrait le solide en équilibre). Dans ce cas-là, les polygones ne sont pas fermés (puisque l'on n'est pas à l'équilibre) ; les extrémités du dynamique donnent le vecteur de la force résultante, et un point de la ligne d'action de la force résultante est donné sur le funiculaire par l'intersection des droites extrêmes.

On peut utiliser la méthode pour trouver le centre de gravité d'un système. En effet, le centre de gravité est l'endroit où on peut appliquer une force mettant le solide en équilibre si celui-ci n'est soumis qu'à son poids. Si le solide est composé de plusieurs parties dont on connaît les centres de gravité et les masses, il suffit de tracer le funiculaire en considérant les poids des différentes parties, et ce pour deux orientations différentes de l'objet ; l'intersection des lignes d'action des résultantes donne la position du centre de gravité. Par simplicité, on fait tourner le funiculaire et le dynamique plutôt que l'objet, et on considère deux directions perpendiculaire (l'horizontale et la verticale).

• Portail de la physique