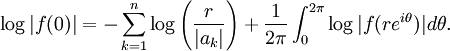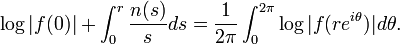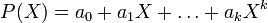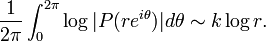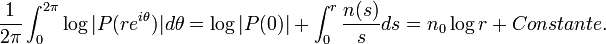Formule de jensen

Formule de Jensen

La formule de Jensen (d'après le mathématicien Johan Jensen) est un résultat d'analyse complexe qui décrit le comportement d'une fonction analytique sur un cercle par rapport aux modules des zéros de cette fonction. Elle est d'une aide précieuse pour l'étude des fonctions entières.

L'énoncé est le suivant:

Soit f est une fonction analytique sur une région du plan complexe contenant un disque fermé D de centre 0 et soit 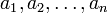$a_1, a_2,\dots,a_n$ les zéros de f dans D, comptés avec leur multiplicité. Si 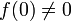$f(0)\ne 0$ , alors

$\log |f(0)| = -\sum_{k=1}^n \log\left(\frac{r}{|a_k|}\right)+\frac{1}{2\pi}\int_0^{2\pi}\log|f(re^{i\theta})|d\theta.$

Ou de manière équivalente :

Si n(r) désigne le nombre de zéros de module <r, alors

$\log |f(0)|+\int_0^r\frac{n(s)}{s}ds=\frac{1}{2\pi}\int_0^{2\pi}\log|f(re^{i\theta})|d\theta.$

Cette formule établit un lien entre les modules des zéros contenus dans un disque $| z | < r$ et les valeurs de $| f (z) |$ sur le cercle $| z | = r$ , et peut être vue comme une généralisation des propriétés de valeurs moyennes des fonctions harmoniques. La formule de Jensen peut être généralisée aux fonctions méromorphes: c'est le théorème de Poisson-Jensen.

Sommaire

1 Applications
- 1.1 Le théorème fondamental de l'algèbre
- 1.2 La théorie des fonctions entières
2 Références

Applications

Le théorème fondamental de l'algèbre

Article détaillé : Théorème de d'Alembert-Gauss.

Le théorème fondamental de l'algèbre affirme que tout polynôme P(X) à coefficients complexes de degré k admet k racines comptées avec multiplicité. Il existe de nombreuses démonstrations plus ou moins équivalentes utilisant des outils d'analyse complexe. Par exemple, la formule de Jensen énoncée plus haut fournit une preuve du théorème fondamental.

Le polynôme P(X) est une série entière dont les coefficients sont nuls pour des indices suffisamment grands :

$P(X)=a_0+a_1X+\dots+a_kX^k$

où a_k est non nul. On peut supposer a₀ non nul. L'application 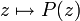$z\mapsto P(z)$ est une fonction holomorphe entière (= définie sur C). On a l'équivalent $P (z)˜ a k z k$ . Par des méthodes classiques de comparaison d'intégrales divergentes, il vient :

$\frac{1}{2\pi}\int_0^{2\pi}\log|P(re^{i\theta})|d\theta \sim k\log r.$

Un polynôme de degré k sur C a au plus k racines complexes comptées avec multiplicité. Comme n(r) est croissant, n(r) est constant égal à n₀ pour r suffisamment grand. La formule de Jensen donne

$\frac{1}{2\pi}\int_0^{2\pi}\log|P(re^{i\theta})|d\theta=\log |P(0)|+\int_0^r\frac{n(s)}{s}ds= n_0\log r+Constante .$

En comparant les deux équivalents obtenus, on obtient $n 0 = k$ . Par conséquent, le polynôme P(X) possède k racines comptées avec multiplicité.

La théorie des fonctions entières

Article détaillé : fonction entière.

La formule de Jensen est fondamentale dans la théorie développée principalement par Nevanlinna pour tout ce qui touche au théorème de Picard.

Références

Complex Analysis, John M. Howie, Springer-Verlag
Complex Analysis, L. V. Ahlfors, McGraw-Hill, 1979, ISBN 0-07-000657-1

Portail des mathématiques

Ce document provient de « Formule de Jensen ».

Catégorie : Analyse complexe

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Formule de jensen de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

Formule De Jensen — La formule de Jensen (d après le mathématicien Johan Jensen) est un résultat d analyse complexe qui décrit le comportement d une fonction analytique sur un cercle par rapport aux modules des zéros de cette fonction. Elle est d une aide précieuse… … Wikipédia en Français
Formule de Jensen — La formule de Jensen (d après le mathématicien Johan Jensen) est un résultat d analyse complexe qui décrit le comportement d une fonction analytique sur un cercle par rapport aux modules des zéros de cette fonction. Elle est d une aide précieuse… … Wikipédia en Français
Jensen — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Jensen est un patronyme d origine scandinave. Il signifie « fils de Jens » (ou Jean en français). Répandu en Norvège et au Danemark. Dans ce… … Wikipédia en Français
Johan Jensen — Johan Ludwig William Valdemar Jensen, surtout connu comme Johan Jensen, (8 mai 1859 à Nakskov – 5 mars 1925 à Copenhague) était un mathématicien et ingénieur danois. Il est surtout connu pour sa fameuse inégalité d … Wikipédia en Français
Championnat International De Formule 3000 1999 — Le championnat international de F3000 1999 a été remporté par l Allemand Nick Heidfeld sur une monoplace de l écurie West Competition. Règlement sportif L attribution des points s effectue selon le barême 10,6,4,3,2,1. Courses de la saison 1999… … Wikipédia en Français
Championnat international de formule 3000 1999 — Le championnat international de F3000 1999 a été remporté par l Allemand Nick Heidfeld sur une monoplace de l écurie West Competition. Règlement sportif L attribution des points s effectue selon le barême 10,6,4,3,2,1. Courses de la saison 1999… … Wikipédia en Français
Championnat international de Formule 3000 1999 — Le championnat international de F3000 1999 a été remporté par l Allemand Nick Heidfeld sur une monoplace de l écurie West Competition. Règlement sportif L attribution des points s effectue selon le barème 10,6,4,3,2,1. Courses de la saison 1999… … Wikipédia en Français
La Formule — (The Formula) est un film américano allemand réalisé par John G. Avildsen, sorti en 1980. Sommaire 1 Synopsis 2 Fiche technique 3 Distribution 4 Lien externe … Wikipédia en Français
Championnat International De Formule 3000 2000 — Le championnat international de F3000 2000 a été remporté par le Brésilien Bruno Junqueira sur une monoplace de l écurie Petrobras. Règlement sportif L attribution des points s effectue selon le barême 10,6,4,3,2,1. Courses de la saison 2000 Date … Wikipédia en Français
Championnat international de formule 3000 2000 — Le championnat international de F3000 2000 a été remporté par le Brésilien Bruno Junqueira sur une monoplace de l écurie Petrobras. Règlement sportif L attribution des points s effectue selon le barême 10,6,4,3,2,1. Courses de la saison 2000 Date … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Formule de jensen

Formule de Jensen

Sommaire