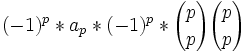Formule d'inversion de pascal
- Formule d'inversion de pascal
-
Formule d'inversion de Pascal
Enoncé et démonstration
Enoncé
Soit 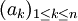 et
et 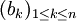 deux familles de réels.
deux familles de réels.
si 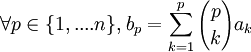
alors 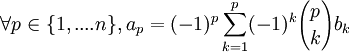
On peut étendre cette formule en remplaçant  par un anneau commutatif quelconque.
par un anneau commutatif quelconque.
Démonstration
On démontre la formule en deux temps.
On montre d'abord le lemme : 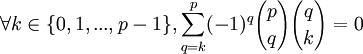
Démonstration du lemme
On doit d'abord montrer que 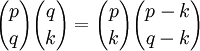
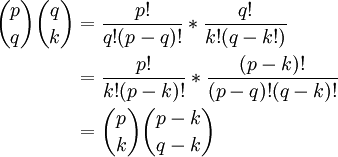
on reprend maintenant l'expression de départ :
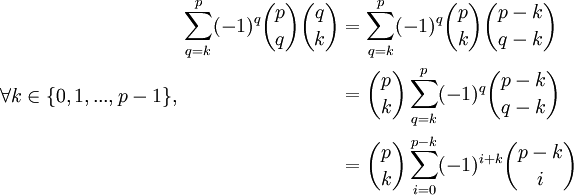
cette quantité vaut bien 0 d'après la formule du binôme de Newton.
Ensuite on démarre avec le membre de droite de la formule, on injecte l'hypothèse, on permute des sommations avant de conclure grâce au lemme.
Démonstration de la formule
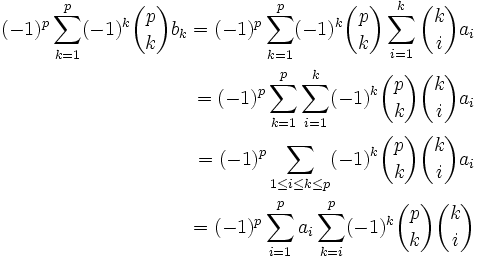
D'après le lemme, tous les termes s'annulent sauf pour 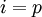 , il reste donc
, il reste donc 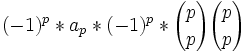
Et on retrouve bien notre ap.
Applications classiques
On peut se servir de cette formule en dénombrement, en particulier pour calculer le nombre de dérangements d'un ensemble fini ou le nombre de surjections d'un ensemble fini vers un autre.
 Portail des mathématiques
Portail des mathématiques
Catégories : Analyse combinatoire | Blaise Pascal
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Formule d'inversion de pascal de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Formule D'inversion De Pascal — Sommaire 1 Enoncé et démonstration 1.1 Enoncé 1.2 Démonstration 2 Applications classiques // … Wikipédia en Français
Formule d'inversion de Pascal — Sommaire 1 Enoncé et démonstration 1.1 Enoncé 1.2 Démonstration 2 Applications classiques 3 … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français
Coefficient binomial — En mathématiques, les coefficients binomiaux, définis pour tout entier naturel n et tout entier naturel k inférieur ou égal à n, donnent le nombre de sous ensembles différents à k éléments que l on peut former à partir d un ensemble contenant n… … Wikipédia en Français
Liste d'équations et formules — Ceci est une Liste des équations et formules par ordre alphabétique. Cette liste contient les équations, les formules, les relations et autres identités, égalités ou inégalités. Sommaire : Haut A B C D E F G H I J K L M N O P Q R S T U V W X … Wikipédia en Français
Liste Des Théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème … Wikipédia en Français
Liste des theoremes — Liste des théorèmes Liste des théorèmes par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le… … Wikipédia en Français
Liste des théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème … Wikipédia en Français
que — 1. que [ kə ] conj. • Xe; lat. médiév. que, forme affaiblie de qui, simplification de quia, employé en bas lat. au sens de quod « le fait que; que » 1 ♦ Introd. une complétive (à l indic. ou au subj. suivant le v. de la principale, ou la nuance à … Encyclopédie Universelle
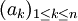 et
et 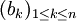 deux familles de réels.
deux familles de réels.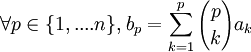
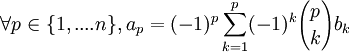
 par un anneau commutatif quelconque.
par un anneau commutatif quelconque.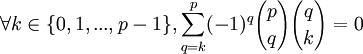 Démonstration du lemme
Démonstration du lemme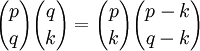
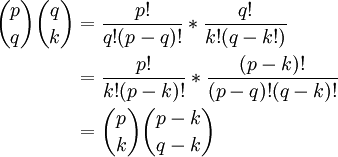
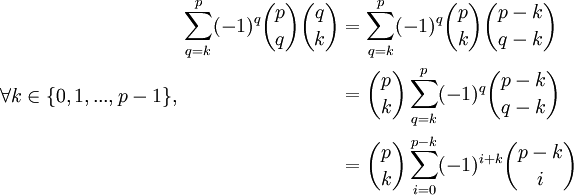
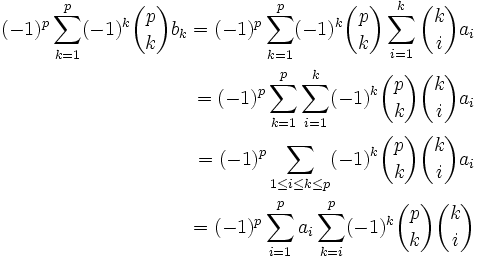
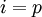 , il reste donc
, il reste donc