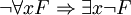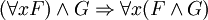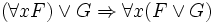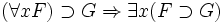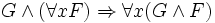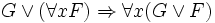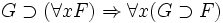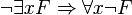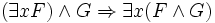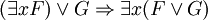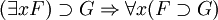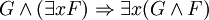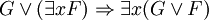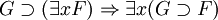Forme Prénexe
- Forme Prénexe
-
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Forme Prénexe de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Forme prenexe — Forme prénexe Une formule de la logique du premier ordre est en forme prénexe si tous ses quantificateurs ( et ) apparaissent à gauche dans cette formule. C’est à dire, G est en forme prénexe ssi avec . Toutes les formules du premier ordre sont… … Wikipédia en Français
Forme prénexe — Une formule de la logique du premier ordre est en forme prénexe si tous ses quantificateurs ( et ) apparaissent à gauche dans cette formule. C’est à dire, G est en forme prénexe si et seulement si avec et une formule sans quantificateurs. Toutes… … Wikipédia en Français
Forme Normale De Skolem — Skolémisation En logique mathématique, la skolémisation d une formule du calcul des prédicats est une transformation de cette formule, qui, dans le cas d une forme prénexe, consiste à éliminer toutes les occurrences de quantificateur existentiel… … Wikipédia en Français
Forme normale de Skolem — Skolémisation En logique mathématique, la skolémisation d une formule du calcul des prédicats est une transformation de cette formule, qui, dans le cas d une forme prénexe, consiste à éliminer toutes les occurrences de quantificateur existentiel… … Wikipédia en Français
Forme normale de skolem — Skolémisation En logique mathématique, la skolémisation d une formule du calcul des prédicats est une transformation de cette formule, qui, dans le cas d une forme prénexe, consiste à éliminer toutes les occurrences de quantificateur existentiel… … Wikipédia en Français
Theoreme de Herbrand — Théorème de Herbrand En logique, le théorème de Herbrand établit un lien entre calcul des prédicats et calcul des propositions. Alors qu il est possible de déterminer de manière certaine si une proposition du calcul des propositions est… … Wikipédia en Français
Théorème de Herbrand — En logique, le théorème de Herbrand établit un lien entre calcul des prédicats et calcul des propositions. Alors qu il est possible de déterminer de manière certaine si une proposition du calcul des propositions est démontrable ou pas, la… … Wikipédia en Français
Théorème de herbrand — En logique, le théorème de Herbrand établit un lien entre calcul des prédicats et calcul des propositions. Alors qu il est possible de déterminer de manière certaine si une proposition du calcul des propositions est démontrable ou pas, la… … Wikipédia en Français
Theoreme de completude de Godel — Théorème de complétude de Gödel Le théorème de complétude du calcul des prédicats du premier ordre a été démontré par Kurt Gödel (1929, thèse de doctorat, sur la complétude du calcul logique). Il affirme que le calcul des prédicats est complet au … Wikipédia en Français
Théorème de complétude — de Gödel Le théorème de complétude du calcul des prédicats du premier ordre a été démontré par Kurt Gödel (1929, thèse de doctorat, sur la complétude du calcul logique). Il affirme que le calcul des prédicats est complet au sens où toute… … Wikipédia en Français
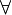 et
et  ) apparaissent à gauche dans cette formule. C’est-à-dire, G est en forme prénexe ssi
) apparaissent à gauche dans cette formule. C’est-à-dire, G est en forme prénexe ssi 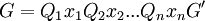 avec
avec 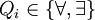 .
.