Fonction additive

En théorie des nombres, une fonction additive est une fonction arithmétique f définie sur l'ensemble des entiers naturels non nuls telle que :

Pour tous a et b entiers naturels non nuls premiers entre eux, f(ab) = f(a) + f(b).

Une fonction arithmétique f est dite complètement additive lorsque :

Pour tous a et b entiers naturels non nuls quelconques, f(ab) = f(a) + f(b),

même si a et b ne sont pas premiers entre eux.

En dehors de la théorie des nombres, le terme additive est habituellement utilisé pour toutes les fonctions vérifiant :

Pour tous a et b entiers naturels non nuls, f(ab) = f(a) + f(b).

Cet article ne concerne que les fonctions additives de la théorie des nombres.

Toute fonction complètement additive est additive, mais la réciproque est fausse.

Exemples

Des exemples de fonctions complètement additives sont :

• La restriction de la fonction logarithme à ℕ^*,
• a₀ : la fonction qui à un entier naturel non nul n associe la somme avec répétition des diviseurs premiers de n (parfois appelée par les anglo-saxons sopfr). Nous avons a₀(20) = a₀(2² ⋅ 5) = 2 + 2+ 5 = 9. Pour avoir quelques valeurs de la fonction, voyez (SIDN A001414) :

a₀(4) = 4 ;

a₀(27) = 9 ;

a₀(144) = a₀(2⁴ ⋅ 3²) = a₀(2⁴) + a₀(3²) = 8 + 6 = 14 ;

a₀(2000) = a₀(2⁴ ⋅ 5³) = a₀(2⁴) + a₀(5³) = 8 + 15 = 23 ;

a₀(2001) = 55 ;

a₀(2002) = 33 ;

a₀(2003) = 2003 ;

a₀(54 032 858 972 279) = 1240658 ;

a₀(54 032 858 972 302) = 1780417 ;

a₀(20 802 650 704 327 415) = 1240681 ;

...

• a₁ : la fonction qui à un entier n associe la somme de ses diviseurs premiers distincts, (parfois appelée par les anglo-saxons sopf). Nous avons a₁(1) = 0, a₁(20) = 2 + 5 = 7. Pour avoir quelques valeurs de la fonction, voyez (SIDN A008472) :

a₁(4) = 2 ;

a₁(27) = 3 ;

a₁(144) = a₁(2⁴ ⋅ 3²) = a₁(2⁴) + a₁(3²) = 2 + 3 = 5 ;

a₁(2 000) = a₁(2⁴ ⋅ 5³) = a₁(2⁴) + a₁(5³) = 2 + 5 = 7 ;

a₁(2 001) = 55 ;

a₁(2 002) = 33 ;

a₁(2 003) = 2003 ;

a₁(54 032 858 972 279) = 1238665 ;

a₁(54 032 858 972 302) = 1780410 ;

a₁(20 802 650 704 327 415) = 1238677.

...

• La fonction Ω, qui associe à un entier naturel non nul n, le nombre total de facteurs premiers qui divisent n, en comptant de multiples fois les facteurs multiples. Nous avons Ω(1) = 0 puisque 1 n'a pas de facteur premier qui le divise. Pour avoir quelques valeurs de la fonction voyez (SIDN A001222) :

Ω(4) = 2 ;

Ω(27) = 3 ;

Ω(144) = Ω(2⁴ ⋅ 3²) = Ω(2⁴) + Ω(3²) = 4 + 2 = 6 ;

Ω(2,000) = Ω(2⁴ ⋅ 5³) = Ω(2⁴) + Ω(5³) = 4 + 3 = 7 ;

Ω(2001) = 3 ;

Ω(2002) = 4 ;

Ω(2003) = 1 ;

Ω(54 032 858 972 279) = 3 ;

Ω(54 032 858 972 302) = 6  ;

Ω(20 802 650 704 327 415) = 7.

...

• Un exemple de fonction arithmétique qui est additive mais pas complètement additive est ω, qui associe à un entier naturel n le nombre total de facteurs premiers distincts qui divisent n. Pour avoir quelques valeurs prises par la fonction voyez (SIDN A001221) (vous pourrez comparer avec Ω) :

ω(4) = 1 ;

ω(27) = 1 ;

ω(144) = ω(2⁴ ⋅ 3²) = ω(2⁴) + ω(3²) = 1 + 1 = 2 ;

ω(2000) = ω(2⁴ ⋅ 5³) = ω(2⁴) + ω(5³) = 1 + 1 = 2 ;

ω(2001) = 3 ;

ω(2002) = 4 ;

ω(2003) = 1 ;

ω(54 032 858 972 279) = 3 ;

ω(54 032 858 972 302) = 5  ;

ω(20 802 650 704 327 415) = 5.

...

Fonctions multiplicatives

À partir de n'importe quelle fonction additive f, il est facile de créer une fonction multiplicative g en définissant par exemple g par :

.

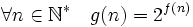Références

1. Janko Bračič, Kolobar aritmetičnih funkcij (Ring of arithmetical functions), (Obzornik mat, fiz. 49 (2002) 4, pp 97 - 108) (MSC (2000) 11A25)

• Portail des mathématiques