Ensemble de besicovitch

Ensemble de besicovitch: Ensemble de Besicovitch

En mathématiques, un ensemble de Besicovitch est un ensemble de point du plan contenant un segment unitaire dans chaque direction et de mesure de Lebesgue nulle.

Sommaire

1 Historique

2 Définition rigoureuse d'un ensemble de Besicovitch

3 Utilisation : le contre-exemple de Besicovitch

4 Construction des ensembles de Besicovitch

4.1 La méthode par dualité

4.2 Une construction concrète

5 Références

Historique

Besicovitch a découvert ces ensembles en 1919 alors qu'il travaillait sur des problèmes d'intégrations dans le plan. La question était de savoir si, étant donnée une fonction Riemann-intégrable dans le plan, il existait toujours une paire d'axes orthogonaux tels que l'on puisse intégrer selon un axe, puis selon l'autre. Les ensembles qu'il découvrit lui permirent d'exhiber un contre-exemple à l'hypothèse précédente.

Définition rigoureuse d'un ensemble de Besicovitch

Un ensemble 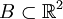$B \subset \mathbb{R}^2$ est appelé ensemble de Besicovitch s'il vérifie les propriétés suivantes :

$B$ contient une segment unitaire dans chaque direction du plan

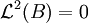
$\mathcal{L}^2(B)=0$

où 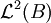$\mathcal{L}^2(B)$ représente la mesure de Lebesgue de $B$ .

La première condition s'exprime aussi : $\forall\ \theta \in \left[0;2\pi\right], \exists\ S$ un segment faisant un angle $θ$ avec l'axe de abscisses.

Remarque : Une autre définition possible consiste à avoir un ensemble contenant une droite dans chaque direction, plutôt qu'un segment.

Utilisation : le contre-exemple de Besicovitch

Nous allons montrer le résultat suivant : il existe une fonction Riemann-intégrable du plan telle que pour toute paire d'axes orthogonaux, l'intégration suivant l'axe des ordonnées soit impossible (au sens de Riemann).

Remarque : on a besoin ici de la compacité (voir Espace compact) de l'ensemble de Besicovitch, qui est assurée par les constructions proposées dans la partie suivante.

Soit 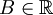$B\in\mathbb{R}$ un ensemble de Besicovitch. On fixe une paire d'axe $(O x 0 y 0)$ grâce à laquelle on définit la fonction 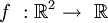$f\ : \mathbb{R}^2 \rightarrow\ \mathbb{R}$ par :

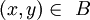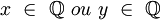Si $(x,y) \in\ B$ et si $x\ \in\ \mathbb{Q}\ ou\ y\ \in\ \mathbb{Q}$ , alors $f (x, y) = 1$ .

Sinon, pour tous les autres éléments de $B$ et tous ceux qui ne sont pas dans $B$ , $f (x, y) = 0$ .

On a en quelque sorte prolongé la fonction caractéristique de $\mathbb{Q}$ sur notre ensemble, en particularisant les points dont l'une au moins des coordonnées est rationnelle. Il faut choisir $(O x 0 y 0)$ de façon à ce que le segment parallèle à $(O x 0)$ (resp. $(O y 0)$ ) soit à distance irrationnelle de cet axe, ce qui est toujours possible.

La compacité de l'ensemble $B$ assure que l'ensemble des points de discontinuité de la fonction $f$ est l'ensemble $B$ lui-même, et est donc de mesure nulle. Le critère de Lebesgue $(1)$ pour les fonctions Riemann intégrable assure que $f$ est Riemann-intégrable sur 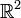$\mathbb{R}^2$ . Nous allons alors montrer que quelle que soit la paire d'axes orthogonaux choisis, on ne pourra pas intégrer $f$ d'abord selon l'axe des ordonnées. Ce qui signifie qu'il existe dans n'importe quel système d'axes orthognaux 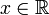$x\in\mathbb{R}$ tel que 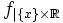$f_{|\{x\}\times\mathbb{R}}$ ne soit pas intégrable au sens de Riemann. Notons 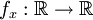$f_x : \mathbb{R}\rightarrow\mathbb{R}$ une telle fonction.

Soit maintenant $(0 x y)$ une paire d'axes orthogonaux quelconque. Soit $x$ l'abscisse du segment parallèle à $(O y)$ et contenu dans $B$ . La fonction $f x$ correspond sur le segment à la fonction caractéristique de $\mathbb{Q}$ . Il est connu que cette fonction n'est pas intégrable, ce qui prouve le résultat.

$(1)$ Toute fonction dont l'ensemble des points de discontinuité est de mesure de Lebesgue nulle est Riemann-intégrable.

Construction des ensembles de Besicovitch

Il existe principalement deux méthodes pour les construire, la méthode historique est celle des triangles, l'autre se basant sur un principe de dualité. On ne présente ici que la construction par dualité. Le principe de la méthode des triangles est d'effectuer des superpositions de triangles pour diminuer progressivement l'aire.

La méthode par dualité

Pour cette méthode, on doit définir une notion de dualité spécifique. A un ensemble de points 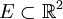$E\subset\mathbb{R}^2$ , on associe l'ensemble de droites $E *$ définit de la façon suivante : 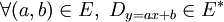$\forall(a,b)\in E,\ D_{y=ax+b}\in E^*$ , où $D y = a x + b$ représente la droite d'équation cartésienne $y = a x + b$ .

Le principe de la construction va être de trouver les propriétés que doit vérifier $E$ pour que $E *$ soit un ensemble de Besicovitch. Plus exactement, on veut que l'ensemble 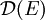$\mathcal{D}(E)$ constitué des supports des droites de $E *$ soit un ensemble de Besicovitch, car formellement $E *$ n'est pas un ensemble de points.

La première propriété d'un ensemble de Besicovitch est de contenir un segment dans chaque direction (ici on a des droites, ce qui revient au même), ce qui équivaut à ce que la projection de $E$ sur $(O x)$ soit l'ensemble $\mathbb{R}$ tout entier.

La deuxième propriété à vérifier est que 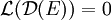$\mathcal{L}(\mathcal{D}(E))=0$ , ce qui implique que la projection de $E$ dans quasiment toutes les directions du plan (c'est-à-dire sauf un nombre fini de directions) soit de mesure de Lebesgue nulle. La démonstration peut être trouvée dans les références.

En conclusion, notre ensemble doit vérifier la condition suivante : la projection dans quasiment toutes les directions du plan doit être de mesure nulle, mais il doit exister une direction particulière telle que la projection dans cette direction soit $\mathbb{R}$ tout entier.

Une construction concrète

Pour réaliser cette construction, on doit exhiber un ensemble vérifiant les propriétés précédentes. Cet ensemble est l'"ensemble de Cantor quatre coins".

Il se construit à partir d'un carré de côté 1 que l'on note $E 0$ . On découpe ce carré en 16 carrés de côté $1 / 4$ , puis on ne garde que les quatre carrés situés dans les coins de $E 0$ : on note ce nouvel ensemble $E 1$ . On réitère le processus sur chacun des quatre carrés de $E 1$ pour obtenir $E 2$ . On construit ainsi pour tout n l'ensemble $E n$ . 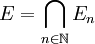L'ensemble de Cantor quatre coins est alors une sorte de limite de cette suite d'ensembles, plus formellement on note : $E = \bigcap_{n\in\mathbb{N}}E_n$ .

On peut montrer que la projection de $E$ sur une droite faisant un angle $arctan(1 / 2)$ avec un côté du carré est un segment, et que pour les autres angles, cette projection a une mesure de Lebesgue nulle. On a donc presque ce que l'on cherche.

On peut maintenant faire en sorte que la projection de $E$ sur l'axe des abscisses soit le segment $[ - 1;1]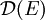$ . $\mathcal{D}(E)$ contient donc une droite de coefficient directeur a pour tout a dans cet intervalle. Si on fait une copie de 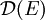$\mathcal{D}(E)$ à laquelle on fait subir une rotation d'angle $π / 2$ , on aura bien un ensemble de Besicovtich.

Références

Kenneth Falconer, The geometry of fractal sets, Cambridge University Press (1985).

Maxime Bourrigan, Autour de la longueur de Favard, rapport de stage sous la direction d'Hervé Pajot (2004).

Disponible en pdf. (page accédée le 7 juillet 2009).

Un autre rapport sur le sujet. (page accédée le 7 juillet 2009).

Portail des mathématiques

Ce document provient de « Ensemble de Besicovitch ».

Catégorie : Théorie de la mesure

Contenu soumis à la licence CC-BY-SA. Source : Article Ensemble de besicovitch de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

Ensemble De Besicovitch — En mathématiques, un ensemble de Besicovitch est un ensemble de point du plan contenant un segment unitaire dans chaque direction et de mesure de Lebesgue nulle. Sommaire 1 Historique 2 Définition rigoureuse d un ensemble de Besicovitch … Wikipédia en Français
Ensemble de Besicovitch — En mathématiques, un ensemble de Besicovitch est un ensemble de points du plan contenant un segment unitaire dans chaque direction et de mesure nulle. Sommaire 1 Historique 2 Définition rigoureuse d un ensemble de Besicovitch 3 … Wikipédia en Français
Ensemble Négligeable — En théorie de la mesure, un ensemble négligeable ou un ensemble de mesure nulle est une partie d un ensemble mesuré dont la définition dépend de la mesure que l on utilise ou plutôt de sa classe d équivalence. À un niveau élémentaire, il est… … Wikipédia en Français
Ensemble de mesure nulle — Ensemble négligeable En théorie de la mesure, un ensemble négligeable ou un ensemble de mesure nulle est une partie d un ensemble mesuré dont la définition dépend de la mesure que l on utilise ou plutôt de sa classe d équivalence. À un niveau… … Wikipédia en Français
Ensemble negligeable — Ensemble négligeable En théorie de la mesure, un ensemble négligeable ou un ensemble de mesure nulle est une partie d un ensemble mesuré dont la définition dépend de la mesure que l on utilise ou plutôt de sa classe d équivalence. À un niveau… … Wikipédia en Français
Ensemble négligeable — Ne pas confondre avec Négligeable en analyse réelle En théorie de la mesure, un ensemble négligeable ou un ensemble de mesure nulle est une partie d un ensemble mesuré dont la définition dépend de la mesure que l on utilise ou plutôt de sa… … Wikipédia en Français
Ensemble rectifiable — En mathématiques, un ensemble rectifiable est une généralisation pluridimensionnelle de courbe rectifiable. Ce sont les objets différentiels de la théorie géométrique de la mesure, fondée par Herbert Federer. Définitions Une partie A de est m… … Wikipédia en Français
Abram Besicovitch — (en russe : Абрам Самойлович Безикович, Abram Samoïlovitch Bezikovitch) (24 janvier 1891 2 novembre 1970) est un mathématicien russe, qui a surtout travaillé en Angleterre. Il est né à Berdiansk au bord de la mer d Azov (aujourd hui en… … Wikipédia en Français
Presque nulle part — Ensemble négligeable En théorie de la mesure, un ensemble négligeable ou un ensemble de mesure nulle est une partie d un ensemble mesuré dont la définition dépend de la mesure que l on utilise ou plutôt de sa classe d équivalence. À un niveau… … Wikipédia en Français
Presque partout — Ensemble négligeable En théorie de la mesure, un ensemble négligeable ou un ensemble de mesure nulle est une partie d un ensemble mesuré dont la définition dépend de la mesure que l on utilise ou plutôt de sa classe d équivalence. À un niveau… … Wikipédia en Français

Mark and share
Search through all dictionaries
Translate…
Search Internet

Share the article and excerpts