Dérivée Fonctionnelle

Dérivée fonctionnelle

La dérivée fonctionnelle est un outil mathématique du calcul des variations.

Soit $F [φ]$ une fonctionnelle, c'est-à-dire une application d'un espace de Banach dans le champ des nombres réels ou complexes. L'objet $\tfrac{\delta F\left[\phi\right]}{\delta\phi(x)}$ , appelé dérivée fonctionnelle ou dérivée de Fréchet, représente la variation $δ F [φ]$ de la fonctionnelle $F [φ]$ rapportée à la variation de la fonction $φ(x)$ au point $x$ . Par conséquent, la dérivée fonctionnelle elle-même dépend de $x$ . On peut adopter comme définition :

$\delta F\left[\phi\right]=\int\mathrm dx \frac{\delta F \left[\phi\right]}{\delta \phi(x)} \delta\phi(x)$ ,

ce qui implique que la variation totale de $F$ sous l'effet de la variation de la fonction $φ(x)$ est une superposition linéaire des changements locaux additionnés sur toute la plage de variation de $x$ .

On peut aussi définir la dérivée fonctionnelle à la façon d'une dérivée classique, comme la limite d'un rapport entre deux variations. Pour montrer cela, on va imposer à la fonction $φ(x)$ une variation de grandeur $ε$ localisée au point $y$ :

$\delta\phi\left[ x\right]=\epsilon \delta(x-y)$

En insérant cela dans la première définition, on obtient :

$\delta F\left[\phi\right]=F\left[\phi+\epsilon\delta(x-y)\right]-F\left[\phi\right]=\int \mathrm dx \frac{\delta F \left[\phi\right]}{\delta \phi(x)} \epsilon\delta(x-y)=\epsilon\frac{\delta F \left[\phi\right]}{\delta \phi(y)}$

En passant à la limite 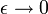$\epsilon\rightarrow 0$ , on a :

$\frac{\delta F \left[\phi\right]}{\delta \phi(y)}=\lim_{\varepsilon \to 0}\frac{F\left[\phi+\varepsilon\delta(x-y)\right]-F\left[\phi\right]}{\varepsilon}$

Règles de calcul

La dérivée fonctionnelle obéit à des règles semblables à celles du calcul différentiel ordinaire :

Elle est linéaire.
La dérivée fonctionnelle d'un produit de deux fonctionnelles $F\left[\phi\right]=G\left[\phi\right]H\left[\phi\right]$ est donnée par :

$\frac{\delta F \left[\phi\right]}{\delta \phi(x)}=\frac{\delta G \left[\phi\right]}{\delta \phi(x)}H\left[\phi\right]+G\left[\phi\right]\frac{\delta H \left[\phi\right]}{\delta \phi(x)}$
La dérivée fonctionnelle d'une fonctionnelle de fonctionnelle est donnée par :

$\frac{\delta}{\delta\phi(y)}F\bigl[G\left[\phi\right]\bigr]=\int\mathrm dx \frac{\delta F\left[G\right]}{\delta G(x)}\frac{\delta G\left[\phi\right]}{\delta \phi (y)}$

En physique

La dérivée fonctionnelle est une technique standard de minimisation (par exemple, minimisation d'un potentiel énergétique). Les calculs ne sont la plupart du temps pas justifiés formellement (d'un point de vue mathématique), la règle informelle suivante étant la plus souvent appliquée:

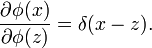
$\frac{\partial \phi(x)}{\partial \phi(z)} = \delta(x-z).$

Cette équation se démontre à partir de l'équation aux limites ci-dessus.

Articles de mathématiques en rapport avec l'analyse fonctionnelle
Fonctionnelle • Calcul des variations • Dérivée fonctionnelle • Espace de Banach • Algèbre de Banach • Espace de Hilbert • Espace de Fréchet • Variété banachique • Espace de fonctions • Noyau reproduisant • Série de Fourier • Transformée de Fourier • Distribution • Topologie faible

Portail des mathématiques

Ce document provient de « D%C3%A9riv%C3%A9e fonctionnelle ».

Catégories : Analyse fonctionnelle | Calcul des variations

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Dérivée Fonctionnelle de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

Derivee fonctionnelle — Dérivée fonctionnelle La dérivée fonctionnelle est un outil mathématique du calcul des variations. Soit F[φ] une fonctionnelle, c est à dire une application d un espace de Banach dans le champ des nombres réels ou complexes. L objet , appelé… … Wikipédia en Français
Dérivée fonctionnelle — La dérivée fonctionnelle est un outil mathématique du calcul des variations. Soit F[ϕ] une fonctionnelle, c est à dire une application d un espace de Banach dans le champ des nombres réels ou complexes. L objet , appelé dérivée fonctionnelle ou… … Wikipédia en Français
Dérivée de Fréchet — Dérivée fonctionnelle La dérivée fonctionnelle est un outil mathématique du calcul des variations. Soit F[φ] une fonctionnelle, c est à dire une application d un espace de Banach dans le champ des nombres réels ou complexes. L objet , appelé… … Wikipédia en Français
Dérivée fractionnaire — Analyse fractionnaire L analyse fractionnaire est une branche de l analyse qui étudie la possibilité qu un opérateur différentiel puisse être élevé à un ordre non entier. On peut définir par ce procédé des dérivées ou des intégrales… … Wikipédia en Français
Dérivée — En analyse, le nombre dérivé en un point d une fonction à variable et valeurs réelles est le coefficient directeur de la tangente au graphe de cette fonction en ce point. C est le coefficient directeur de l approximation affine de cette fonction… … Wikipédia en Français
Fonctionnelle hybride — Une fonctionnelle hybride est un élément d une classe d approximations à la fonctionnelle d échange corrélation, introduite en 1993 par Axel Becke[1], utilisé au sein de la théorie de la fonctionnelle de la densité (DFT). La caractéristique de… … Wikipédia en Français
Analyse fonctionnelle (mathématiques) — Pour les articles homonymes, voir Analyse fonctionnelle. L analyse fonctionnelle est la branche des mathématiques et plus particulièrement de l analyse qui étudie les espaces de fonctions. Elle prend ses racines historiques dans l étude des… … Wikipédia en Français
Theorie de la fonctionnelle de la densite — Théorie de la fonctionnelle de la densité Méthodes numériques pour le calcul de la structure électronique Hartree Fock Théorie de la perturbation de Møller Plesset Interaction de configuration Méthode du cluster couplé Champ multi… … Wikipédia en Français
Théorie de la fonctionnelle de la densité — Pour les articles homonymes, voir DFT. La théorie de la fonctionnelle de la densité (pour Density Functional Theory, sous entendu électronique : DFT) constitue au début du XXIe siècle l une des méthodes les plus utilisées dans les… … Wikipédia en Français
Théorie de la fonctionnelle densité — Théorie de la fonctionnelle de la densité Méthodes numériques pour le calcul de la structure électronique Hartree Fock Théorie de la perturbation de Møller Plesset Interaction de configuration Méthode du cluster couplé Champ multi… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Dérivée Fonctionnelle