- Double optique
-
Une étoile double optique est un couple d'étoiles apparemment proches mais dont les deux composantes sont en réalité séparées par une grande distance. Elles apparaissent comme double visuelle à cause de leur proximité apparente en projection sur le ciel et ce ne sont donc pas des vraies étoiles binaires liées gravitationnellement.
Historiquement, le débat pour savoir si toutes les étoiles doubles observées étaient ou non des doubles optiques s'est essentiellement déroulé à partir du milieu du XVIIIe siècle (Lambert, Michell) et sera clos par William Herschel en 1803 avec la mise en évidence des premières étoiles binaires.
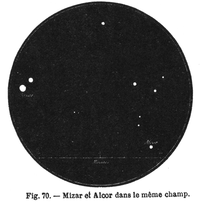Mizar A et B (à gauche) sont vraisemblablement un couple physique, tandis que Mizar avec Alcor (droite) forment peut-être un couple optique. Figure de Camille Flammarion (1882)
Pour prouver que deux étoiles forment réellement un couple physique et non un couple optique, il faut avoir mis en évidence leur orbite, ce qui peut prendre des siècles, ou bien montrer qu'elles sont proches parce que l'on a une indication de leur distance ou vitesse. Inversement, si l'on observe un déplacement relatif qui est uniforme et linéaire entre les deux composantes, c'est qu'il s'agit probablement d'un couple optique dont on voit le mouvement propre de chacune des composantes.
Faute d'indications observationnelles de ce type permettant de trancher quant à la nature du couple, il reste la possibilité d'un test statistique, avec le risque d'erreur naturellement associé. On peut évaluer ainsi quelle est la probabilité d'avoir un objet à la séparation angulaire ρ (en secondes d'arc) de l'étoile considérée, sa présence étant due au hasard seul. Il est clair que la probabilité de se trouver en présence d'une double optique augmente avec la densité stellaire sur le plan du ciel (par ex. en direction du très dense centre de notre Galaxie), avec la distance (par ex. en direction d'une galaxie résolue), quand l'instrument utilisé a un bon pouvoir de résolution et que les observations sont profondes en magnitude apparente.
Avec l'hypothèse simplificatrice que les étoiles ont dans une petite zone du ciel une densité surfacique uniforme D (en nombre d'étoiles par seconde d'arc carrée jusqu'à la magnitude apparente m), la probabilité d'avoir au moins une étoile de magnitude m dans l'élément de surface π ρ² autour d'une étoile donnée est obtenue avec la loi de Poisson par :
- P(ρ,m)=1-exp(-π ρ2 D)
Par exemple, avec la résolution d'un instrument comme le Télescope spatial Hubble, et en direction du centre galactique dans la très dense fenêtre de Baade, on peut escompter observer environ 3 millions d'étoiles par degré carré dans le visible à la magnitude 20, soit une chance sur 2 d'avoir au moins une étoile plus brillante que 20 à moins d'une seconde d'arc d'une étoile donnée ; en revanche, en direction des pôles galactiques, cette probabilité retombe à une chance sur mille. Donc, si l'on a un couple séparé par une seconde d'arc, il est très probable que ce soit un couple optique dans le premier cas, mais beaucoup moins dans le second.
Voir aussi
Liens internes
Wikimedia Foundation. 2010.
