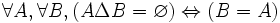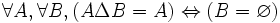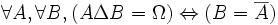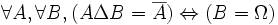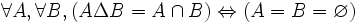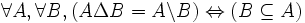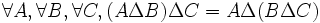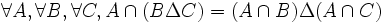- Différence symétrique
-
Algèbre des parties d'un ensemble
Cet article est consacré à une première approche des opérations sur les ensembles et de leurs propriétés : réunion, intersection, différence, complémentation, différence symétrique...
Sommaire
Réunion
Définition
Pour tout ensemble A et tout ensemble B, il existe un ensemble U dont les éléments sont ceux de A et de B ( cette proposition, qui est un axiome implicite de la théorie naïve des ensembles, découle, dans la théorie des ensembles de l'axiome de la paire et de l'axiome de la réunion ). En notation symbolique :
L'unicité de l'ensemble U est garantie par l'axiome d'extensionnalité. On le note « A U B » ( lire « A union B » ), et on l'appelle réunion de A et de B.
Propriétés
- U1 ( commutativité ) : la réunion de deux ensembles ne dépend pas de l'ordre dans lequel ces deux ensembles sont pris. En notation symbolique :
- U2 ( Ø élément neutre ) : la réunion de l'ensemble vide avec un ensemble quelconque redonne cet ensemble. En notation symbolique :
- U3 ( idempotence ) : la réunion d'un ensemble quelconque avec lui-même redonne cet ensemble. En notation symbolique :
- U4 : tout ensemble est inclus dans sa réunion avec un autre ensemble. En notation symbolique :
- U5 : un ensemble A est inclus dans un ensemble B si et seulement si leur réunion est égale à B. En notation symbolique :
- U6 : si la réunion de deux ensembles est vide, alors ils sont vides tous les deux. En notation symbolique :
- U7 ( compatibilité avec l'inclusion ) : la réunion de deux sous-ensembles est incluse dans la réunion des deux ensembles dont ils sont sous-ensembles. En notation symbolique :
- U8 ( associativité ) : le résultat de la réunion de plusieurs ensembles ne dépend pas de l'ordre dans lequel les opérations de réunion sont faites. En notation symbolique :
Intersection
Définition
Pour tout ensemble A et tout ensemble B, il existe un ensemble S dont les éléments sont ceux qui sont communs à A et à B. Cette proposition, qui est un axiome implicite de la théorie naïve des ensembles, découle, dans la théorie des ensembles, du schéma d'axiomes de compréhension. En notation symbolique :
L'unicité de l'ensemble S est garantie par l'axiome d'extensionnalité. On le note « A ∩ B » ( lire « A inter B » ), et on l'appelle intersection de A et de B.
Propriétés
- N1 ( commutativité ) : l'intersection de deux ensembles ne dépend pas de l'ordre dans lequel ces deux ensembles sont pris. En notation symbolique :
- N2 ( Ø élément absorbant ) : l'intersection de l'ensemble vide et d'un ensemble quelconque est vide. En notation symbolique :
- N3 ( idempotence ) : l'intersection d'un ensemble quelconque avec lui-même redonne cet ensemble. En notation symbolique :
- N4 : l'intersection de deux ensembles est incluse dans chacun de ces deux ensembles. En notation symbolique :
- N5 : un ensemble A est inclus dans un ensemble B si et seulement si leur intersection est égale à A. En notation symbolique :
- N6 : l'équivalent de U6 se traduit par une définition, celle des ensembles disjoints ( voir ci-dessous ).
- N7 ( compatibilité avec l'inclusion ) : l'intersection de deux sous-ensembles est incluse dans l'intersection des deux ensembles dont ils sont sous-ensembles. En notation symbolique :
- N8 ( associativité ) : le résultat de l'intersection de plusieurs ensembles ne dépend pas de l'ordre dans lequel les opérations sont faites. En notation symbolique :
Cas des familles d'ensembles
Il est possible de définir l'intersection d'une famille quelconque d'ensembles
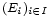 comme l'intersection des ensembles composant cette famille :
comme l'intersection des ensembles composant cette famille :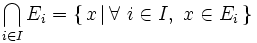 .
.
En particulier, pour une famille vide d'ensembles,
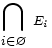 est la « classe » de tous les ensembles et n'est donc pas un ensemble.
est la « classe » de tous les ensembles et n'est donc pas un ensemble.Ensembles disjoints
Deux ensembles sont disjoints si et seulement si leur intersection est vide, c'est-à-dire s'ils n'ont pas d'éléments en commun. Par exemple, si A = { 1, 2 } et B = { 3, 4 }, alors A ∩B = Ø, et A et B sont donc disjoints.
Il existe deux manières de généraliser cette définition à plus de deux ensembles :
- les éléments d'un ensemble E sont (globalement) disjoints si et seulement si l'ensemble noyau de E est vide :
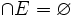 ;
; - les éléments d'un ensemble E sont mutuellement disjoints ou disjoints deux à deux si et seulement si l'ensemble noyau de toute paire de ces éléments est vide, c'est-à-dire si :
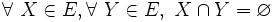 ;
;
Ces deux notions sont différentes : si des ensembles disjoints deux à deux sont globalement disjoints, des ensembles globalement disjoints ne le sont pas nécessairement deux à deux.
Liens avec la réunion
- UN1 ( distributivité de l'intersection par rapport à la réunion ) : l'intersection de la réunion de deux ensembles avec un troisième ensemble est égale à la réunion de l'intersection de chacun des deux premiers ensembles avec le troisième :
- UN2 ( distributivité de la réunion par rapport à l'intersection ) : la réunion de l'intersection de deux ensembles avec un troisième ensemble est égale à l'intersection de la réunion de chacun des deux premiers ensembles avec le troisième :
Démonstration de UN1De chaque côté de l'égalité (UN1) figure un ensemble et nous voulons démontrer que ces ensembles sont égaux. Une stratégie possible pour démontrer cette égalité est de montrer que chaque côté est un sous-ensemble de l'autre.
- Prenons un élément x appartenant à l'ensemble de gauche. Alors, par définition de ∩, x est dans A et x est dans B ∪ C; c'est-à-dire, x est dans A et aussi x est dans B ou x est dans C (ou les deux). Dans le premier cas, x est à la fois dans A et dans B, il est donc dans A ∩ B et « a fortiori » dans (A ∩ B) ∪ (A ∩ C). Dans le second cas, x est à la fois dans A et dans C et donc il est de nouveau dans (A ∩ B) ∪ (A ∩ C). Donc, dans les deux cas, x est dans (A ∩ B) ∪ (A ∩ C). Nous avons montré que tout élément de l'ensemble de gauche est nécessairement dans l'ensemble de droite. Cela correspond exactement à l'inclusion de gauche à droite.
- Prenons un élément de x dans l'ensemble du membre de droite de l'égalité. Alors x est dans A ∩ B ou x est dans A ∩ C (ou les deux). Dans le premier cas, x est dans A et x est dans B; dans le deuxième, x est dans A et x est dans C. Dans les deux cas, x est dans A. Mais dans le premier cas x est dans B et donc dans B ∪ C; dans le deuxième cas, x est dans C et donc encore dans B ∪ C. Nous avons prouvé que quel que soit x, s'il appartient à l'ensemble de droite, alors, il est à la fois dans A et dans B ∪ C et donc par définition il est dans A ∩ (B ∪ C). Nous avons démontré l'inclusion de droite à gauche.
(1) et (2) réunis prouvent que l'ensemble de gauche est égal à l'ensemble de droite, comme prévu.
Démonstration de UN2Nous pouvons démontrer l'égalité (UN2) de la même manière que pour (UN1), par double inclusion.
- Soit x un élément de A ∪ (B ∩ C). x appartient alors à A ou à (B ∩ C). Dans le premier cas, x appartient à la fois à A ∪ B et à A ∪ C. Il appartient donc à (A ∪ B) ∩ (A ∪ C). Dans le deuxième cas, x appartient à la fois à B et à C. Il appartient donc à la fois à A ∪ B et à A ∪ C, c'est-à-dire à (A ∪ B) ∩ (A ∪ C). Dans tous les cas, x est bien un élément de (A ∪ B) ∩ (A ∪ C). Nous avons démontré l'inclusion de gauche à droite.
- Prenons maintenant x un élément de (A ∪ B) ∩ (A ∪ C). D'une part x appartient à A ∪ B, ce qui signifie qu'il appartient à A ou à B. D'autre part, x appartient à A ∪ C. Donc soit x appartient à A, soit x appartient à C et dans ce cas x appartient à A ∩ C ou à B ∩ C. En somme x appartient à A ou à A ∩ C ou à B ∩ C. S'il appartient à A ∩ C, alors il appartient forcément à A. Donc x appartient à A ou à B ∩ C, ce qui signifie que x appartient à A ∪ (B ∩ C). On obtient l'inclusion de gauche à droite.
Les inclusions démontrées dans (1) et (2) entre les deux membres de (UN2) prouvent leur égalité.
Différence
Définition
Pour tout ensemble A et tout ensemble B, il existe un ensemble D dont les éléments sont ceux de A qui n'appartiennent pas à B ( cette proposition, qui est un axiome implicite de la théorie naïve des ensembles, découle, dans la théorie des ensembles du Schéma d'axiomes de compréhension ). En notation symbolique :
L'unicité de l'ensemble D est garantie par l'axiome d'extensionnalité. On le note « A \ B » ( lire « A moins B » ), et on l'appelle différence de A et de B.
« Faire la différence » de deux ensembles A et B se dit aussi « soustraire » B de A.
Propriétés
- D1 ( Ø élément neutre à droite ) : soustraire l'ensemble vide d'un ensemble redonne cet ensemble :
- D2 ( Ø élément absorbant à gauche ) : soustraire un ensemble de l'ensemble vide donne l'ensemble vide :
- D3 ( involutivité ) : soustraire un ensemble de lui-même donne l'ensemble vide :
- D4 : soustraire un sur-ensemble d'un ensemble donne l'ensemble vide, ou, en d'autres termes, pour tout A et tout B, la différence de A et de B est vide si et seulement si A est inclus dans B :
- D5 : soustraire un ensemble d'un autre ne redonne cet ensemble que si et seulement si les deux ensembles sont vides :
- D6 : les deux ensembles intervenant dans une différence ne sont interchangeables sans modification du résultat que s'ils sont égaux :
- D7 : soustraire un ensemble B d'un ensemble A ne redonne A que si et seulement si les deux ensembles sont disjoints :
- D8 : soustraire un ensemble B d'un ensemble A ne donne leur intersection que si et seulement si A est vide :
- D9 : soustraire un ensemble B d'un ensemble A ne donne leur réunion que si et seulement si B est vide :
- D10 : si on soustrait un ensemble B d'un ensemble A, le résultat est un sous-ensemble de A :
- D11 ( pseudo-distributivité à droite en intersection de la différence par rapport à elle-même ) : soustraire successivement deux ensembles B et C d'un ensemble A revient à prendre l'intersection des différences de A et de B, et de A et de C :
- D12 : soustraire d'un ensemble A la différence de deux ensembles B et C revient à prendre la réunion de la différence de A et de B, et de l'intersection de A et de C :
- D13 : réunir un ensemble C avec la différence de deux ensembles A et B revient à soustraire la différence de B et de C de la réunion de A et de C :
- D14 : soustraire un ensemble C de l'intersection de deux ensembles A et B revient à prendre l'intersection de A avec la différence de B et de C :
- D15 ( distributivité à droite de la différence par rapport à l'intersection ) : soustraire un ensemble C de l'intersection de deux ensembles A et B revient à prendre l'intersection de la différence de chacun de ces ensembles avec C :
- D16 ( distributivité à droite de la différence par rapport à la réunion ) : soustraire un ensemble C de la réunion de deux ensembles A et B revient à prendre la réunion de la différence de chacun de ces ensembles avec C :
- D17 ( pseudo-distributivité à gauche en réunion de la différence par rapport à l'intersection ) : soustraire l'intersection de deux ensembles B et C d'un ensemble A revient à prendre la réunion de la différence de A avec chacun des ensembles B et C :
- D18 ( pseudo-distributivité à gauche en intersection de la différence par rapport à la réunion ) : soustraire la réunion de deux ensembles B et C d'un ensemble A revient à prendre l'intersection de la différence de A avec chacun des ensembles B et C :
Cette dernière propriété peut en fait se déduire des précédentes. D14 et D15 peuvent être rapprochées, de même que D12 et D17.
Complémentaires
Définitions
Article détaillé : Complémentaire (théorie des ensembles).Deux ensembles B et C sont complémentaires dans un ensemble A si
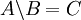 .
.Pour tout ensemble A et tout ensemble B, si B est inclus dans A, alors A \ B se note aussi « A - B » (lire encore « A moins B »), et s'appelle complémentaire relatif de B dans A.
Si Ω désigne un référentiel, et A un ensemble (forcément inclus dans le référentiel), alors Ω - A désigne le complémentaire absolu de A. Il est noté habituellement
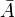 (lire « A barre » ou « non A »).
(lire « A barre » ou « non A »).Propriétés
- PROPOSITION 4 : B et C sont complémentaires dans A si et seulement si C est le complémentaire relatif de B dans A :
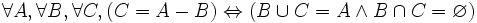
- PROPOSITION 5 : Pour tout ensemble universel Ω et sous-ensembles A et B de Ω:
-
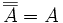 ;
;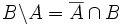 ;
;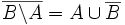 ;
;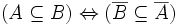 ;
;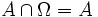 ;
;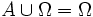 ;
;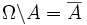 ;
;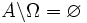 ;
;
Différence symétrique
Définition
Pour tout ensemble A et tout ensemble B, il existe un ensemble D dont les éléments sont ceux qui appartiennent soit à A, soit à B, mais pas aux deux à la fois: en effet, c'est la différence de A U B et de A ∩ B . En notation symbolique :
On le note « A Δ B » (lire « A delta B »), et on l'appelle différence symétrique de A et de B.
- ( rappel :
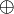 désigne le ou exclusif logique )
désigne le ou exclusif logique )
Il existe deux autres définitions équivalentes :
Cette dernière définition justifie l'appellation de différence symétrique donnée à cette opération.
Propriétés
- DS1 (commutativité) : la différence symétrique de deux ensembles ne dépend pas de l'ordre dans lequel ces ensembles sont pris :
- DS2 (Ø élément neutre) : la différence symétrique de l'ensemble vide et d'un autre ensemble redonne cet ensemble :
- DS3 (involutivité) : la différence symétrique de tout ensemble avec lui-même donne l'ensemble vide :
Cette propriété a pour conséquence immédiate :
- DS4 (inversibilité) : pour tout ensemble, il en existe un tel que leur différence symétrique soit vide :
Cette propriété a à son tour pour conséquence :
- DS5 (régularité) : si les différences symétriques d'un ensemble avec deux autres ensembles sont égales entre elles, alors ces deux autres ensembles sont égaux entre eux :
- DS6 (Ω élément inverseur) : la différence symétrique d'un ensemble et du référentiel donne le complément absolu de cet ensemble :
- DS7 : la différence symétrique d'un ensemble et de son complément absolu redonne le référentiel :
- DS8 : le complément absolu de la différence symétrique de deux ensembles est égal à la différence symétrique de l'un des deux ensembles avec le complément absolu de l'autre ensemble :
- DS9 : pour tout A et tout B, A \ B et B \ A forment une partition de A Δ B :
- DS10 : pour tout A et tout B, A Δ B et A ∩ B forment une partition de A U B :
- DS11 : la différence symétrique de deux ensembles est vide si et seulement si les deux ensembles sont égaux :
- DS12 : la différence symétrique de deux ensembles est égale à l'un des deux ensembles si et seulement si l'autre ensemble est vide :
- DS13 : la différence symétrique de deux ensembles est égale au référentiel si et seulement si les deux ensembles sont complémentaires absolus :
- DS14 : la différence symétrique de deux ensembles est égale au complément absolu de l'un d'entre eux si et seulement si l'autre ensemble est le référentiel :
- DS15 : la différence symétrique de deux ensembles est égale à leur intersection si et seulement si les deux ensembles sont vides :
- DS16 : la différence symétrique de deux ensembles est égale à leur réunion si et seulement s’ils sont disjoints :
- DS17 : la différence symétrique de deux ensembles est égale à la différence de l'un avec l'autre si et seulement si l'un est inclus dans l'autre :
- DS18 (associativité) : la différence symétrique de trois ensembles ne dépend pas de l'ordre dans lequel les opérations sont effectuées :
- DS19 (distributivité de ∩ par rapport à Δ) : l'intersection d'un ensemble avec la différence symétrique de deux autres ensembles est égale à la différence symétrique des intersections du premier ensemble avec chacun des deux autres :
Exemples
Pour illustrer ces notions, soient A l'ensemble des personnes gauchères, et B l'ensemble des personnes blondes.
Alors A ∩ B est l'ensemble de tous les gauchers blonds, alors que A ∪ B est l'ensemble de toutes les personnes qui sont ou gauchères ou blondes, ou les deux. A \ B, en revanche, est l'ensemble de toutes les personnes qui sont gauchères mais pas blondes, alors que B \ A est l'ensemble de toutes personnes blondes mais pas gauchères. Enfin, A Δ B désigne l'ensemble de toutes les personnes soit blondes, soit gauchères, mais pas les deux à la fois.
Maintenant supposons que E soit l'ensemble de tous les êtres humains, et que F l'ensemble de tous ceux qui sont âgés de plus de 1000 ans. Qu'est-ce que E ∩ F dans ce cas? Aucun humain n'a plus de 1000 ans, donc E ∩ F doit être l'ensemble vide : Ø.
Nous avons énuméré sans démonstration plusieurs propriétés simples des opérations sur les ensembles. Ces propriétés peuvent être visualisées avec les diagrammes de Venn.
Voir aussi
- Opération ensembliste
- Théorie naïve des ensembles
- Ensemble
- Sous-ensemble
- Produit cartésien
- Correspondance et relation
- Portail des mathématiques
Catégorie : Théorie des ensembles
Wikimedia Foundation. 2010.

![\forall\ A , \forall\ B , \exists\ U / \, \forall\ X ,\ ( X \in U ) \Leftrightarrow [ ( X \in A ) \vee ( X \in B ) ] \,](/pictures/frwiki/102/f4b91942247e209a140f7fc6b603c080.png)
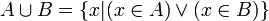
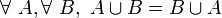
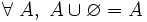
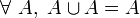
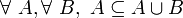
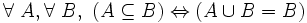
![\forall\ A , \forall\ B ,\ [ A \cup B = \varnothing ] \Rightarrow [ ( A = \varnothing ) \wedge ( B = \varnothing ) ] \,](/pictures/frwiki/48/0e85f0e5a268ef092d650920fde6f893.png)
![\forall\ A , \forall\ B , \forall\ C , \forall\ D ,\ [ ( A \subseteq B ) \wedge ( C \subseteq D ) ] \Rightarrow [ ( A \cup C ) \subseteq ( B \cup D ) ] \,](/pictures/frwiki/53/5fae4c4b501a99d5b4b19536011eb57c.png)
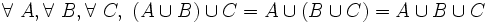
![\forall\ A , \forall\ B , \exist\ S /\, \forall\ X ,\ ( X \in S ) \Leftrightarrow [ ( X \in A ) \wedge ( X \in B ) ] \,](/pictures/frwiki/49/1dc46410383c9e6e01100abf58c8b870.png)
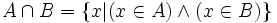
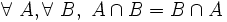
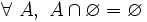
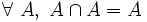
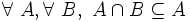
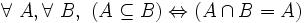
![\forall\ A , \forall\ B , \forall\ C , \forall\ D ,\ [ ( A \subseteq B ) \wedge ( C \subseteq D ) ] \Rightarrow [ ( A \cap C ) \subseteq ( B \cap D ) ] \,](/pictures/frwiki/101/e03a1eb54cd7c1cc3098a6e415aaac3d.png)
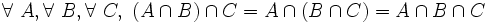
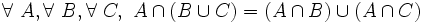
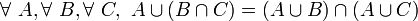
![\forall\ A , \forall\ B , \exist\ D /\, \forall\ X ,\ ( X \in D ) \Leftrightarrow [ ( X \in A ) \wedge ( X \not\in B ) ] \,](/pictures/frwiki/50/2de8ef5a778c375ebe99ff5f4c857e05.png)
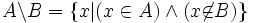
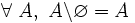
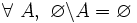
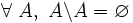
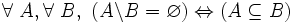
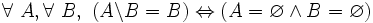
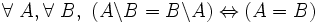
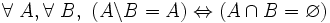
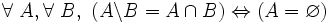
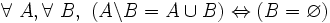
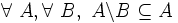
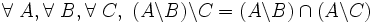
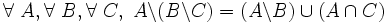
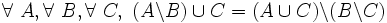
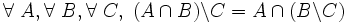
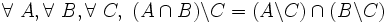
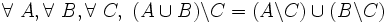
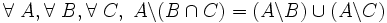
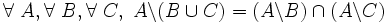
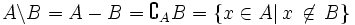
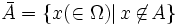
![\forall A, \forall B, \exists D / \,\forall X, (X \in D) \Leftrightarrow [(X \in A) \Leftrightarrow (X \not\in B)]](/pictures/frwiki/97/a2da85d1bdf74b0a336733a060c134f3.png)
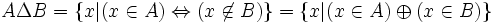
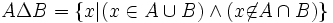
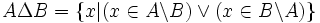
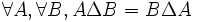
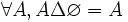
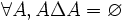
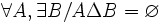
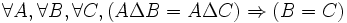
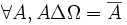
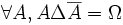
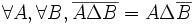
![\forall A, \forall B, [\, A \Delta B = ( A \backslash B ) \cup ( B \backslash A ) \,] \wedge [ \,( A \backslash B ) \cap ( B \backslash A ) = \varnothing \,]](/pictures/frwiki/50/27e545059079d7c2ceb9ec5de8c330c6.png)
![\forall A, \forall B, [ \,A \cup B = ( A \Delta B ) \cup ( A \cap B ) \,] \wedge [\, ( A \Delta B ) \cap ( A \cap B ) = \varnothing \,]](/pictures/frwiki/53/50a62361c5b3b51aecafeb6bbf74f3ab.png)