Denavit-Hartenberg

Denavit-Hartenberg

Denavit et Hartenberg (D-H) est une convention[précision nécessaire] habituellement utilisée pour choisir le système de référence en robotique. Elle fut introduite[Quand ?] par Jacques Denavit et Richard S. Hartenberg. Selon cette convention, chaque transformation[précision nécessaire] est représentée comme le produit de quatre transformations basiques.

Pour définir ces transformations, il est tout d'abord nécessaire de définir les axes des liaisons :

  1. Les axes \vec{z_n} sont suivant les axes des liaisons.
  2. Les axes \vec{x_n} sont parallèles à la normale commune à \vec{z_{n - 1}} et \vec{z_n} soit : \vec{x_n} = \vec{z_{n-1}} \wedge \vec {z_{n}} .
  3. Les axes \vec{y_n} sont choisi de manière à former un trièdre direct avec les axes \vec{z_n} et \vec{x_n}.
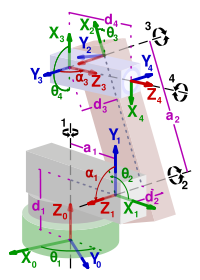Exemple de la chaîne cinématique d'un robot avec système de coordonnées et paramètres selon Denavit&Hartenberg.


Chaque transformation entre deux corps successifs est donc décrite par quatre paramètres :

  1. d, la distance selon l'axe \vec{z_n} entre les axes \vec{x_{n}} et \vec{x_{n+1}}
  2. θ, l'angle entre autour de l'axe \vec {z_{n}} entre les axes \vec{x_{n}} et \vec{x_{n+1}}
  3. r, la distance selon l'axe \vec{x_n} entre les axes \vec{z_{n-1}} et \vec{z_{n}}. C'est donc également la longueur de la normale commune.
  4. α, l'angle entre autour de l'axe \vec {x_{n}} entre les axes \vec{z_{n-1}} et \vec{z_{n}}


En multipliant les matrice de rotation et de translation élémentaire, on peut obtenir la transformation globale entre deux liaisons successives qui s'écrit :

T=\begin{pmatrix} cos(\theta) & -cos(\alpha) sin(\theta) & sin(\alpha) sin(\theta) & r cos(\theta)\\ sin(\theta) & cos(\alpha) cos(\theta) & -cos(\theta) sin(\alpha) & r sin(\theta)\\ 0 & sin(\alpha) & cos(\alpha) & d\\ 0 & 0 & 0 & 1\\ \end{pmatrix}.

On peut calculer formellement la matrice inverse :

T^{-1}=\begin{pmatrix} cos(\theta) & sin(\theta) & 0 & -r \\ -cos(\alpha) sin(\theta) & cos(\alpha) cos(\theta) & sin(\alpha) & -d sin(\alpha) \\ sin(\alpha) sin(\theta) & -cos(\theta) sin(\alpha) & cos(\alpha) & -d cos(\alpha) \\ 0 & 0 & 0 & 1\\ \end{pmatrix}

Articles connexes


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Denavit-Hartenberg de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Denavit-Hartenberg-Transformation — Beispiel einer kinematischen Kette anhand eines Roboters; mit Koordinatensystemen und DH Parametern Die Denavit Hartenberg Transformation (DH Transformation) aus dem Jahr 1955 ist ein mathematisches Verfahren, das auf der Basis von homogenen… …   Deutsch Wikipedia

  • Denavit–Hartenberg parameters — A commonly used convention for selecting frames of reference in robotics applications is the Denavit and Hartenberg (D–H) convention which was introduced by Jaques Denavit and Richard S. Hartenberg. In this convention, each homogeneous… …   Wikipedia

  • Denavit-Hartenberg Parameters — A commonly used convention for selecting frames of reference in robotics applications is the Denavit and Hartenberg (D H) convention which was introduced by Jaques Denavit and Richard S. Hartenberg. In this convention, each homogeneous… …   Wikipedia

  • Robotics conventions — There are many conventions used in the robotics research field. This article summarises these conventions. Contents 1 Line representations 2 Non minimal vector coordinates 2.1 Plücker coordinates …   Wikipedia

  • Robotertechnik — Roboter sind stationäre oder mobile Maschinen, die nach einem bestimmten Programm festgelegte Aufgaben erfüllen. Allerdings hat sich die Bedeutung im Laufe der Zeit gewandelt. Der Begriff Roboter (tschechisch: robot) wurde von Josef und Karel… …   Deutsch Wikipedia

  • Vorwärtstransformation — Die direkte Kinematik oder Vorwärtstransformation ist ein Begriff aus der Robotik. Sie befasst sich mit der Frage, wie aus den Gelenkwinkeln der Armelemente eines Industrieroboters die Pose (Position und Orientierung) des Endeffektors (engl.:… …   Deutsch Wikipedia

  • Direkte Kinematik — Die direkte Kinematik oder Vorwärtstransformation ist ein Begriff aus der Robotik. Sie befasst sich mit der Frage, wie aus den Gelenkwinkeln der Armelemente eines Industrieroboters die Pose (Position und Orientierung) des Endeffektors (engl.:… …   Deutsch Wikipedia

  • Industrierobotik — Ein Industrieroboter ist eine universelle, programmierbare Maschine zur Handhabung, Montage oder Bearbeitung von Werkstücken. Diese Roboter sind für den Einsatz im industriellen Umfeld konzipiert (z. B. Automobilfertigung). Die Maschine besteht… …   Deutsch Wikipedia

  • Roboter — sind stationäre oder mobile Maschinen, die nach einem bestimmten Programm festgelegte Aufgaben erfüllen. Allerdings hat sich die Bedeutung im Laufe der Zeit gewandelt. Der Begriff Roboter (tschechisch: robot) wurde von Josef und Karel Čapek… …   Deutsch Wikipedia

  • Schweißroboter — Ein Industrieroboter ist eine universelle, programmierbare Maschine zur Handhabung, Montage oder Bearbeitung von Werkstücken. Diese Roboter sind für den Einsatz im industriellen Umfeld konzipiert (z. B. Automobilfertigung). Die Maschine besteht… …   Deutsch Wikipedia

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”