Critère de routh

Critère de routh

Polynôme de Hurwitz

Un polynôme à coefficients réels, de degré n, est appelé polynôme de Hurwitz si les n racines complexes sont toutes à partie réelle négative.

On montre aisément que nécessairement, tous les coefficients du polynôme sont de même signe, et donc sans restreindre la généralité, on prend le terme constant T0 égal à 1 en physique.

Sommaire

Résultats pour n<5

n=2 : pas d'autre condition (évident pour un physicien habitué au circuit RLC).

n=3 : rajouter : ET T2.T1 − T3.T0 > 0

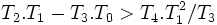
n=4 : rajouter : ET T_2.T_1 - T_3.T_0 > T_4.T_1^2/T_3

Remarque : pour un physicien, les coefficientsTn sont des constantes de temps à la puissance n. Il pourra aisément contrôler l'homogénéité des formules.

Le cas n = 3 se retient aisément par des considérations énergétiques (voir l'article filtre électrique linéaire).

Le cas n=4 se retient mnémotechniquement aisément grâce au cas n=3 : effectivement si T4 est quasi-nul, on devait retrouver n=3 . Par contre, il faut connaître la situation de 2 oscillateurs couplés avec injection de puissance, pour intuiter aisément l'inéquation T2.T1 / T3.T0 > 1 + k.(T4 / T0).(T1 / T3)2, k=1 .

Au-delà, il vaut mieux traiter la question par l'algorithme des tableaux de Routh. Néanmoins, une remarque de pertinence : si P(x) est de Hurwitz, x^n .P(1/x) est de Hurwitz : les conditions sont donc « symétriques » sur les coefficients.

Par exemple, le cas n= 5 se retient assez aisément: il y a deux inégalités:

A: = (T4.T3 − T5.T2) > 0

évidemment et

B2 − A.C < 0

avec B: = (T4.T1 − T5.T0)

et

C: = (T2.T1 − T3.T0)

Un théorème facile

Soit P(x) le polynôme, de degré n, dont on veut savoir s'il est polynôme de Hurwitz ; et soit Q(x) le polynôme de degré (élevé !) n(n-1)/2 dont les racines sont les sommes deux à deux des racines de P(x).

Pour que P(x) soit de Hurwitz , il faut et suffit que tous les coefficients de Q(x) soient positifs.

Démonstration : la condition est nécessaire ; en effet, les parties réelles des n(n-1)/2 racines de Q(x) sont négatives ; et en regroupant les racines conjuguées, le résultat apparaît.

La condition est suffisante : en effet, Q(x), à coefficients tous positifs, n'a pas de racine réelle positive (règle évidente de Descartes : Q(x)>0 si x >0).Or, raisonnant par l'absurde, SI P(x) avait 2 racines conjuguées a+ bI et a-bI avec a>0 , alors 2a (>0) serait racine de Q(x) : Contradiction. Donc toutes les racines de P(x) ont leur partie réelle négative.

Dans le cas n=3 et donc n(n-1)/2 = 3 , il est ainsi facile pour un non-physicien de faire le calcul et de retrouver l'inégalité précédente.

Le cas n=4 est un peu plus difficile, mais en fait un beau raisonnement de Lienard et Chipart permet de se ramener à n=3 !

Le cas n=5 conduit à un polynôme Q(x) de degré 10 : il est temps d'utiliser l'algorithme des tableaux de Routh, même si un physicien spécialiste des oscillations essaie de vous persuader que les 2 inéquations sont nécessaires pour raison de transfert énergétique et de contre-réaction.


Cas général : les tableaux de Routh et critère de Routh-Hurwitz

Le tableau de Routh est un critère de stabilité utilisé en automatique. Il permet de déterminer, au regard du dénominateur de la fonction de transfert en boucle fermée, si le système bouclé, représenté par cette fonction, est stable ou non (cf stabilité EBSB).

Soit s la variable de la fonction de transfert. Le dénominateur s'écrit sous la forme d'un polynôme en s :

ansn + an − 1sn − 1 + ... + a0

  • Condition nécessaire :
 tous les coefficients ai doivent être non nuls
 tous les coefficients ai doivent être de même signe

Rem : autre manière de dire : ao = 1 et tous les coefficients strictement positifs.

Si ces 2 conditions ne sont pas réunies, le système est instable.

Pour déterminer en plus la condition suffisante, il nous faut dresser le tableau de Routh.

La 1e ligne du tableau, indexée par sn, comporte les coefficients an, an − 2,....

La 2e ligne du tableau, indexée par sn − 1, comporte les coefficients an − 1, an − 3,...

Puis pour les autres lignes, on complète de la manière suivante :

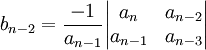
1e colonne de la 3e ligne : b_{n-2}=\frac{-1}{a_{n-1}}\begin{vmatrix} a_{n} & a_{n-2} \\ a_{n-1} & a_{n-3} \end{vmatrix}

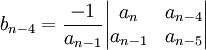
2e colonne de la 3e ligne : b_{n-4}=\frac{-1}{a_{n-1}}\begin{vmatrix} a_{n} & a_{n-4} \\ a_{n-1} & a_{n-5} \end{vmatrix}

ect.... (si on ne peut pas compléter une case, on y met un zéro)

ce qui nous donne le tableau suivant :


Tableau de Routh
sn
an
an − 2
 an − 4
sn − 1
an − 1
an − 3
 an − 5
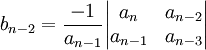
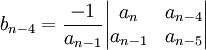
sn − 2 b_{n-2}=\frac{-1}{a_{n-1}}\begin{vmatrix} a_{n} & a_{n-2} \\ a_{n-1} & a_{n-3} \end{vmatrix} b_{n-4}=\frac{-1}{a_{n-1}}\begin{vmatrix} a_{n} & a_{n-4} \\ a_{n-1} & a_{n-5} \end{vmatrix}
...
sn − 3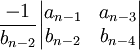
\frac{-1}{b_{n-2}}\begin{vmatrix} a_{n-1} & a_{n-3} \\ b_{n-2} & b_{n-4} \end{vmatrix}
...
...


  • Condition nécessaire et suffisante :

si tous les coefficients de la 1e colonne sont tous non nuls et de même signe alors le système bouclé est stable.


Remarque : la condition nécessaire et suffisante de stabilité pour un système du 2e ordre est que tous les coefficents soient de même signe (on obtient simplement ce résultat en appliquant le critère de Routh)


Exemple : af''(t) + bf(t) = 0 avec a > 0


si b > 0 alors les coefficents sont de même signe donc le système est stable. En effet, la solution f(t) est :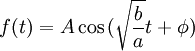 f(t) = A\cos{(\sqrt{\frac{b}{a}}t+\phi)}

f(t) est alors bornée comme l'entrée (ici 0) donc le système est stable.


si b < 0, le système est instable. En effet, la solution est :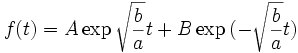 f(t) = A\exp{\sqrt{\frac{b}{a}}t} + B\exp{(-\sqrt{\frac{b}{a}}t)}

qui diverge lorsque t tend vers l'infini.

Intérêt pour la physique

La stabilité d'un système d'oscillateurs linéaires est liée à celle de son polynôme caractéristique, à coefficients réels positifs. Idem pour les filtres électriques linéaires.

Pour qu'un système soit stable, il faut que son polynôme caractéristique ait toutes ses racines à partie réelle négative. Cela revient à dire que ce polynôme est un polynôme de Hurwitz. Il importe donc de trouver les conditions à réaliser par les coefficients pour qu'il en soit ainsi.

Ce problème naît avec acuité dès qu'un moteur injecte une puissance au système, donc avec le développement de la machine à vapeur, et plus particulièrement du régulateur de James Watt (1736-1819). Sa solution va mobiliser l'élite des mathématiciens du XIXe siècle : Charles Sturm (1803-1855), Cauchy (1789-1857), Hurwitz (1859-1919), etc.

Bibliographie

Benidir et Barrett, stabilité des filtres et des systèmes linéaires, Dunod1999, ISBN 2 10 004432 X :256p, plutôt mathématique, niveau maîtrise, il complète un article d'histoire des sciences :

M. Barret, « Historique depuis Cauchy jusqu'à Fujiwara des solutions au problème de la localisation des zéros d'un polynôme dans le plan complexe », Prépublication de l'Institut de recherche mathématique avancée, vol. 22, Strasbourg 1996. Niveau : professeur de mathématiques.

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Polyn%C3%B4me de Hurwitz ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Critère de routh de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

  • critère de Routh — Routh o stabilumo kriterijus statusas T sritis automatika atitikmenys: angl. Routh s criterion vok. Routh Kriterium, n rus. критерий устойчивости Рауса, m pranc. critère de Routh, m ryšiai: sinonimas – Rauso stabilumo kriterijus …   Automatikos terminų žodynas

  • Critere de routh — Polynôme de Hurwitz Un polynôme à coefficients réels, de degré n, est appelé polynôme de Hurwitz si les n racines complexes sont toutes à partie réelle négative. On montre aisément que nécessairement, tous les coefficients du polynôme sont de… …   Wikipédia en Français

  • Critere de routh-hurwitz — Polynôme de Hurwitz Un polynôme à coefficients réels, de degré n, est appelé polynôme de Hurwitz si les n racines complexes sont toutes à partie réelle négative. On montre aisément que nécessairement, tous les coefficients du polynôme sont de… …   Wikipédia en Français

  • Critère de routh-hurwitz — Polynôme de Hurwitz Un polynôme à coefficients réels, de degré n, est appelé polynôme de Hurwitz si les n racines complexes sont toutes à partie réelle négative. On montre aisément que nécessairement, tous les coefficients du polynôme sont de… …   Wikipédia en Français

  • Routh'o stabilumo kriterijus — statusas T sritis automatika atitikmenys: angl. Routh s criterion vok. Routh Kriterium, n rus. критерий устойчивости Рауса, m pranc. critère de Routh, m ryšiai: sinonimas – Rauso stabilumo kriterijus …   Automatikos terminų žodynas

  • Routh's criterion — Routh o stabilumo kriterijus statusas T sritis automatika atitikmenys: angl. Routh s criterion vok. Routh Kriterium, n rus. критерий устойчивости Рауса, m pranc. critère de Routh, m ryšiai: sinonimas – Rauso stabilumo kriterijus …   Automatikos terminų žodynas

  • Routh-Kriterium — Routh o stabilumo kriterijus statusas T sritis automatika atitikmenys: angl. Routh s criterion vok. Routh Kriterium, n rus. критерий устойчивости Рауса, m pranc. critère de Routh, m ryšiai: sinonimas – Rauso stabilumo kriterijus …   Automatikos terminų žodynas

  • Critere de hurwitz — Polynôme de Hurwitz Un polynôme à coefficients réels, de degré n, est appelé polynôme de Hurwitz si les n racines complexes sont toutes à partie réelle négative. On montre aisément que nécessairement, tous les coefficients du polynôme sont de… …   Wikipédia en Français

  • Critère de hurwitz — Polynôme de Hurwitz Un polynôme à coefficients réels, de degré n, est appelé polynôme de Hurwitz si les n racines complexes sont toutes à partie réelle négative. On montre aisément que nécessairement, tous les coefficients du polynôme sont de… …   Wikipédia en Français

  • Edward Routh — Edward John Routh (20 janvier 1831 – 7 juin 1907), est un mathématicien anglais. E. Routh Sommaire 1 Biographie …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”